0. 논리회로 요약

Intro

해당 내용은 컴퓨터 구조를 더 잘 이해하기 위해서 논리회로의 내용을 축약하여 정리한 포스팅이다.

컴퓨터 회로에서는 모든 연산이 이진수로 이루어진다. 그 이유는 높은 전압이 흐를 때를 1, 그렇지 않을 때를 0으로 정의를 하여 이를 통해서 값을 구분하기 때문이며, 이것이 우리가 이진수 체계에서 컴퓨터 연산을 표현하는 이유이다.

만약, 이를 삼진수 이상으로 표현할 수 있다면, 더 획기전 연산이 가능하겠지만, 비용적인 측면과 물리적인 측면에서 아직은 한계가 있다. (양자 컴퓨터 역시 이와 유사한 원리이다.)

해당 분야에서는 0->1로 바뀌는 것을 active(활성화)시켰다고 한다. 또한, 0인 상태를 deasserted signal, 1인 상태를 asserted signal이라고 한다.

Truth Table(진리표)

이진수로 표현되는 값의 input과 이를 통한 output을 나타내기 위해서 우리는 진리표를 활요한다. 여기서는 A,B가 input, C가 output이 된다. C는 A와 B를 OR 연산한 결과이다.

Gate

그림은 위에서 부터 AND, OR, NOR, NAND, 그리고 input을 뒤집는 inversion Gate를 나타낸 것이다.

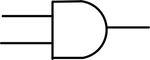
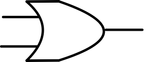
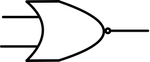
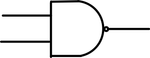
각 Gate는 다음과 같은 연산을 출력한다.

1. AND 2 inputs / 1 output

$0 \cdot0 = 0 \\ 0 \cdot1 = 0 \\ 1 \cdot0 = 0 \\ 1 \cdot1 = 1$

2. OR 2 inputs / 1 output

$0 + 0 = 0 \\ 0 + 1 = 1 \\ 1 + 0 = 1 \\ 1 + 1 = 1$

3. NOR 2 inputs / 1 output

$\overline{(0 + 0)} = 1 \\ \overline{(0 + 1)} = 0 \\ \overline{(1 + 0)} = 0 \\ \overline{(1 + 1)} = 0$

4. NAND 2 inputs / 1 output

$\overline{(0 \cdot0)} = 1 \\ \overline{(0 \cdot1)} = 1 \\ \overline{(1 \cdot0)} = 1 \\ \overline{(1 \cdot1)} = 0$

5. Inversion(=NOT) 1 inputs / 1 output

$\overline{1} = 0 \\ \overline{0} = 1$

여기서 하나 특별한 개념이 나온다. 바로 Functional Complete이다. 특정 Gate만 가지고, 위에서 제시된 모든 연산을 표현할 수 있으면, 이를 Functional Complete라고 한다. 여기서 우리는 가장 보편적으로 생각할 수 있는 {AND, OR, NOT}는 모두 표현할 수 있다는 것을 알 수 있다. 그런데, 여기서 {NAND} 하나만 가지고 이를 표현할 수 있는데, 아래가 이에 대한 예시이다.

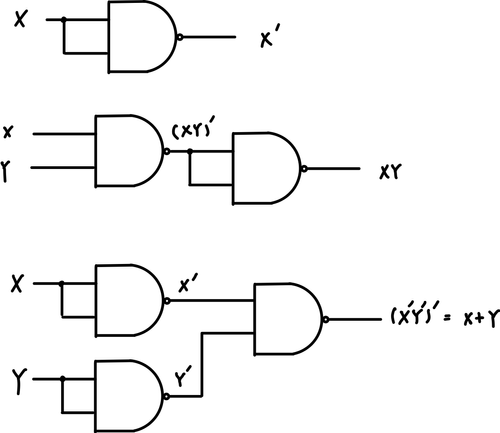
그리고, {NOR}만 가지고도 똑같이 표현가능하다.

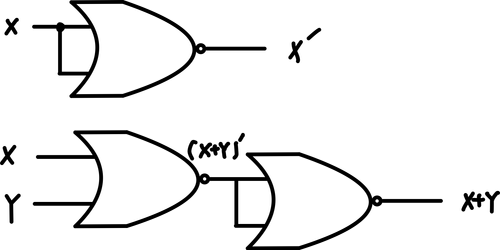
동일한 값을 NAND, NOR하면 역수가 나온다는 특징과 드 모르간의 법칙에 의해서 이것이 정의된다고 할 수 있다.

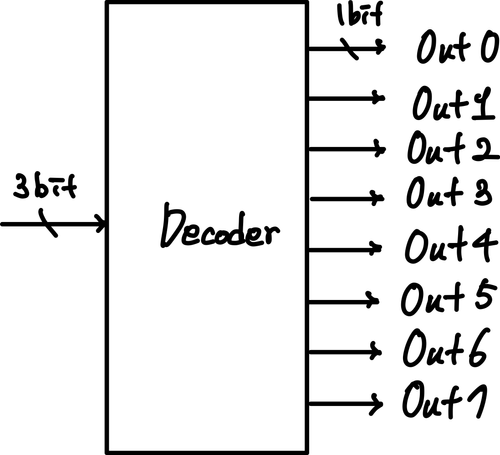
Decoder

n bit로 표현할 수 있는 $2^{n}$개의 값을 회선을 통해서 표현하기 위해서 $2^{n}$개의 회선 중에서 단 하나의 값만 active한다.

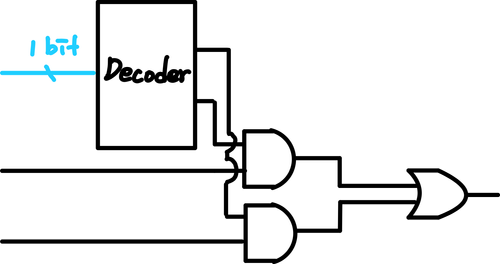
Multiplexor(=Selector)

Control에 의해서 선택되어진 Input을 Output으로 내보낸다. 이를 위해서 Input 여러 개와 이 중에 무엇을 선택할지를 의미하는 Selector(=Control) Value을 입력한다. 형태는 input의 갯수만큼의 AND Gate와 Output Gate, 그리고 Decoder로 이루어진다.

1. Decoder를 통해서 Signal Bit를 나눈다.
2. 각 Input의 크기만큼 Decoder의 각 Input의 크기를 확장하여 AND 연산을 취한다.
3. 나온 모든 결과를 OR로 연산한다.

Clock

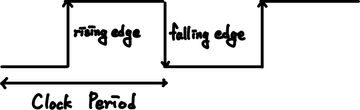
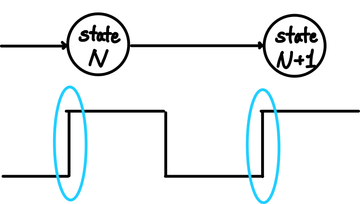
Clock이란 고정된 Cycle time을 주기로 하여 발생하는 신호를 의미한다. 여기서 고정된 Cycle Time은 Clock이 높은 시점과 낮은 시점으로 구분할 수 있다. 우리의 모든 연산은 Clock이 감소하거나 증가하는 그 시점에 동작한다. 이를 Edge Triggered Clocking이라고 부른다. 따라서, 우리는 정확히 상태값이 변하는 edge에서를 active 상태라고 부르는데 이를 오르는 edge로 할지 내려가는 edge로 할지는 설계자의 몫이다.

하나의 Clock이 의미하는 것은 특정 상태에서 연산이 이루어져서 다음 단계로 넘어간다는 의미이다. 따라서, Clock Period가 짧을 수록, 다음 상태로 빠르게 넘어갈 수 있다. 하지만, 이를 무한정으로 올리는 것은 불가능하며, 열이 너무 증가하여 회로 전체에 악영향을 줄 수도 있다.

Latches

걸쇠를 의미하며, 값을 저장해놓는다는 의미를 가진다. 이를 이용해서 Memory와 같은 저장장치를 만들 때 사용한다. 두 가지 형태가 존재하니 하나씩 알아보자. (물론 자세히 알면 좋겠지만 필자는 이정도 개념이 있다는 정도로만 기억한다.)

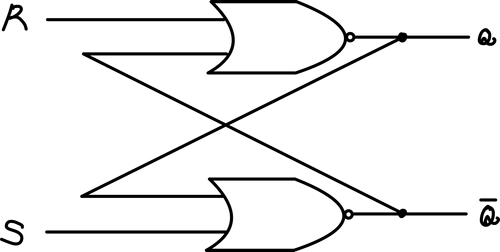
S-R Latch(Set Reset Latch)

S와 R이 모두 0이면 값이 변하지 않고, Cross되는 위치에 데이터가 저장되게 된다. R(Reset)만 1로 하면, 데이터 값이 0으로 초기화된다. S(Set)만 1로 하면, 데이터 값이 1로 세팅된다. R과 S를 모두 1로 하면 해당 값은 저장이라는 의미를 갖지 못한다.

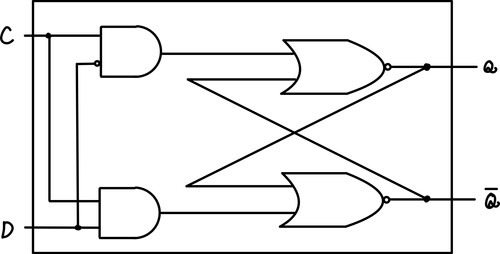
D Latch

Clock단위로 데이터를 저장하기 위해서 이와 같은 장치를 이용한다. 하지만, 이는 Clock이 asserted된 상태(1)인 상태에 언제든지 변환된다는 특징을 갖고 있다. Output은 저장되어있는 값과 등일하다.

Flip-Flop

Clock단위로 데이터를 저장하기 위해서 이와 같은 장치를 이용한다. 하지만, 이는 Clock이 변화하는 edge에서만 상태가 변한다는 특징을 갖고 있다. Output은 저장되어있는 값과 동일하다. 아래는 대표적인 D Flip-Flop이다.

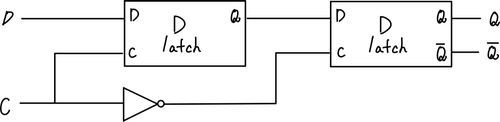
실제로는 Latch보다 Flip Flop을 이용하는 것이 일반적인데, 왜 그렇게 하는 것일까? 이는 우리가 입력을 받을 때, 이를 처리하기 위한 최소하의 시간이 필요하기 때문이다.

이 최소한의 시간은 다음과 같이 정의된다.

$t_\text{prop} + t_\text{combinational} + t_\text{setup} + t_\text{skew}$

1. $t_\text{prop}$ : flip-flop 내에서 신호가 처리되는데 까지 걸리는 시간을 의미한다.
2. $t_\text{combinational}$ : 실제 연산이 수행되는 부분이다.
3. $t_\text{setup}$ : 전기적 신호가 바로 low에서 high로 이동하는 것이 아니기 때문에 이를 setup하는데 걸리는 시간을 의미한다.
4. $t_\text{skew}$ : 공정과정에서 완벽하게 만들더라도 각 소자마다 어느정도 차이가 발생하게 되는데 이를 의미한다.

이처럼 이 시간동안 우리는 다른 처리를 수행할 수 없다. 따라서, 이것을 처리하는 동안의 시간을 확보하기 위해서 우리는 Edge에서만 수행하는 방식을 사용하고 있다. 또한, Clock Cycle Time 또한 이보다는 크게 setting하는 것이 일반적이다.