Dynamic Programming

Intro

Dynamic Programming은 기본적으로 이전에 계산했던 데이터를 여러 번 사용할 때 적은 시간 비용으로 문제를 해결할 수 있는 알고리즘입니다. 이를 정의하기 위해서 Overlapping Subproblem, Optimal Structural 라는 단어를 주로 사용하며 이에 대해 살펴보겠습니다.

정의

우리말로 동적 계획법이라고 번역되어지는 말입니다. 우선 명칭에 대해서 좀 어색할 수 있다. 이는 해당 어원이 오래되었기 때문입니다. 당시에 programming이란 문제 풀이를 위한 planning(계획) 정도로 생각했습니다. 따라서, Dynamic Programming이 의미하는 바는 다단계 처리에 대한 최적화된 계획법 정도로 해석할 수 있습니다.

Dynamic Programming을 사용하기 위해서는 해당 문제가 다음과 같은 조건을 만족할 때입니다.

Optimal Substructure
Overlapping Subproblem

Optimal Substructure란 문제의 최적해가 이것의 하위 문제(subproblem)의 최적해에 의해서 정의되어질 수 있어야 한다는 것입니다. 쉽게 말해서 수열의 경우 점화식을 작성할 수 있어야 한다는 의미입니다. 가장 일반적인 예시가 fibonacci 수열을 예로 들 수 있습니다.

$fibo(n) = fibo(n-1) + fibo(n-2)$

Overlapping Subproblem이란 문제의 하위 문제(subproblem)들이 중첩해서 사용되는 경우를 말합니다. 위의 fibonacci 수열만 보아도 fibo(100)은 fibo(101), fibo(102)를 계산하기 위해서 쓰이기 때문에 중복이 발생하며, 더 나아가 fibo(101), fibo(102)를 사용하는 경우에는 fibo(100)을 다시 계산해야 합니다. 이것은 굉장한 비용을 초례합니다.

이러한 문제들에 대한 해결책으로써 Dynamic Programming에서는 점화식을 이용해서 문제를 해결하지만, 이때, 한 번 계산한 값을 두 번 계산하지 않도록 하는 것입니다. 이를 가능하게 하는 것이 Memoization(함수의 실행 결과를 저장)입니다. 즉, 이전에 호출한 함수의 결과값을 별도의 저장 공간(array, list, map, file 등)에 저장해두는 것입니다. 이를 통해서 우리는 problem의 subproblem이 이미 계산된 적이 있다면, 하위 문제를 다시 풀 필요없이 바로 solution(점화식)을 계산할 수 있는 것입니다. 이를 통해서, 계산 시간을 획기적으로 줄일 수 있습니다. 하지만, 추가적인 memory를 사용한다는 점을 반드시 기억해야 합니다.

여기서 계속해서 반복 및 교체되어 사용되는 단어가 점화식, solution, optimal substructure, function, 함수입니다. 이는 모두 같은 뜻을 가지는데, 여기서도 특히 함수는 referential transparency를 보장하는 함수만을 지칭합니다. 수학에서는 아주 당연한 얘기이지만, input값이 동일할 때 항상 같은 output을 내놓아야 한다는 것입니다. programming에서의 함수는 대게 side effect가 존재할 수 있고, 외부 변수를 사용하기도 하므로, 같은 input이라도 상황(context)에 따라 다른 output이 발생할 수도 있는데 이러한 것이 해당 함수에서는 발생해서는 안된다는 것입니다.

구현

기본적으로 Dynamic Programming을 적용하기 위해서는 반드시 위에서 언급한 두 조건을 만족하는지를 확인해야 합니다. 따라서, 먼저 점화식을 찾아내고, 이것이 반복 사용되는지를 반드시 확인한 후에 적용하는 것이 기본입니다.

Dynamic Programming의 기본적인 구현 방식은 두 가지가 존재합니다. 둘 다 장단점이 있기 때문에 이것에 유의하여 사용해야 합니다.

따라서, 아래에서는 가장 기본적인 예시로 combination을 구하는 방식을 두 가지 방식으로 구현하겠습니다. 일단 Combination은 다음과 같은 점화식을 만족합니다.

${{}_{n}C_{k}} = {{}_{n-1}C_{k-1}} + {{}_{n-1}C_{k}}$

따라서, 이를 Dynamic Programming을 통해서 구현할 수 있습니다.

1. Top Down(=Recursive)

먼저 input으로 들어올 데이터의 크기를 고려하여, cache list의 크기를 지정합니다. 그 후에 점화식을 함수 내에서 나타내고, 해당 함수값을 return해주면 됩니다. 이때 중요한 것이 이미 함수값을 계산한 적이 있는지를 확인하고 있다면, 바로 return해버리는 점입니다.


1size = 100
2# 1차원 배열
3cache = [-1] * size
4
5# 2차원 배열
6cache = [[-1 for _ in range(size)] for _ in range(size)]
7
8# 기저값 세팅
9cache[0][0] = 1
10cache[1][0] = 1
11cache[1][1] = 1
12
13# 함수 지정
14def recursive_call(a, b):
15    # 이미 저장된 값이 있는 경우 return
16    if cache[a][b] != -1:
17        return cache[a][b]
18    # 없다면, 연산 및 저장 후 return
19    cache[a][b] = cache[a-1][b-1] + cache[a-1][b]
20    return cache[a][b]
21    
22print(recursive_call(10, 2))

해당 방식의 가장 큰 장점은 이해하기 쉽다는 것입니다. 점화식이 분명하게 들어나며, 값을 찾아가는 과정을 상상하는 것이 쉽습니다. 또한, 모든 경우의 수를 탐색하지 않을 수 있다는 점이 있습니다. 왜냐하면, 연관된 데이터만 찾기 때문에 관련 없는 데이터는 찾지 않을 수도 있습니다. 하지만, recursive call인 만큼 함수 호출의 최대 횟수가 정해져있어, 모든 경우에 올바른 답을 찾지는 못합니다. 이를 해결하기 위해서 끊어서 실행 시켜두는 방법도 있습니다. 예를들어 200을 구하는 문제면, 50, 100, 150을 미리 호출해둡니다. 하지만, 이 또한, 매번 적용할 수 있는 방법은 아니기에 대다수의 경우에는 Bottom Up으로 구현하는 것을 추천합니다.

2. Bottom Up(with Loop)

위와 똑같은 원리를 이용해서 구현한 Combination입니다. for문을 이용해서 처음부터 끝까지 구하면서 올라가는 방식입니다. 이렇게 하게 되면, 빈틈없이 아래부터 계산하는지를 체크하면서 구현해야합니다. 중간에 빈값이 발생하는 경우가 없도록 하는 것이 중요합니다.


1size = 100
2# 1차원 배열
3cache = [-1] * size
4
5# 2차원 배열
6cache = [[-1 for _ in range(size)] for _ in range(size)]
7
8# 기저값 세팅
9cache[0][0] = 1
10cache[1][0] = 1
11cache[1][1] = 1
12
13# 함수 지정
14for i in range(2, size):
15 for j in range(0, i+1):
16     cache[i][j] = cache[i-1][j-1] + cache[i-1][j]
17    
18print(cache[10][2])

문제 풀이

모든 Dynamic Programming 문제를 풀기 위해서 거쳐야 하는 단계는 총 3단계입니다.

문제를 정의한다.
점화식을 찾는다.
시간 복잡도를 만족하는지 확인한다.
공간 복잡도를 만족하는지 확인한다.

문제를 정의하고, 점화식을 찾을 때에 나타나는 대략 4가지 유형을 나누어 보았습니다. 제가 만든 분류기준이니 공식적이지는 않습니다.

1. 자신의 Subproblem으로만 표현되는 유형

A = operate(sub A, sub A)와 같은 형태로 나타나는 경우를 말한다. 이 경우에는 문제의 재정의가 필요없이 바로 점화식을 작성하면 됩니다. 이런 유형의 문제가 위에서 살펴보았던 combination, fibonacci가 대표적입니다. 가장 기본적인 예시를 풀어봅시다.

백준 11726

*문제를 읽고 오시기 바랍니다.

11726번: 2×n 타일링

먼저 이 문제는 2xN 평면에 타일을 채울 수 있는 경우의 수를 찾는 것이 목표입니다.

따라서, $cache[n] = \text{2xN을 채울 수 있는 경우의 수}$ 라고 정의하겠습니다.

또한, 규칙을 찾아보면 해당 값은 다음과 같은 pattern을 가진다는 것을 알 수 있습니다.

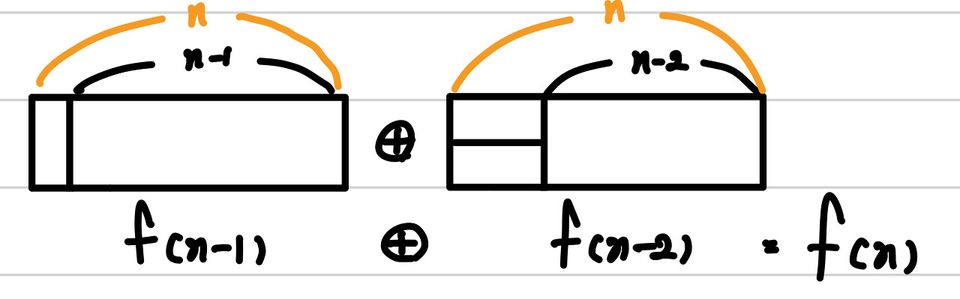
tile_2_1

f(n)의 처음 시작을 세로 block으로 시작하면, 다음 block들의 경우의 수는 모두 이전에 구한 경우의 수와 같고, 처음 block을 가로 block으로 설정하면, 위에 block을 놓으면 아래도 가로로 놓는 것이 강제됩니다. 따라서, 가로로 위 아래를 두는 수 밖에 없고, 이렇게 두면 이전전에 두었던 것과 동일한 형태로 놓는 경우의 수만큼의 경우를 갖게 됩니다. 따라서, 결론상 현재의 block의 경우의 수는 이렇게 두 개의 경우의 수의 합으로 정의할 수 있는 것입니다.

관련 유형 : 1463, 11727, 11052, 16194, 15988, 1699, 2193

2. 문제의 재정의가 필요한 유형

A = operate(B), A' = operate(sub B, sub B)와 같은 형태로 나타나는 경우를 말한다. 이와 같은 유형은 기존에 제시된 문제에 특정 조건을 추가하여, 최종값을 구한 후에 이를 이용해서 답을 구하는 방식입니다. 이 경우에는 문제를 다시 정의해야 하기 때문에 다소 어려울 수 있습니다. 쉬운 예제부터 풀어보겠습니다.

백준 1912

1912번: 연속합

이 문제는 점화식으로 나타기가 어렵습니다. 따라서, 약간 문제를 바꾸어서 나타내야 합니다. 수열을 A라 하고, 수열의 i번째 원소를 A[i]라고 할 때, A[i]를 마지막 연속 합의 값으로 했을 때, 최댓값을 S[i]라고 합시다. 이 경우에 이전의 연속합이 음수인 경우는 오히려 값이 낮아지기 때문에 이때는 A[i]를 반환하고, 그렇지 않은 경우에는 S[i-1]에 A[i]를 더해서 연속합을 구하면 됩니다. 따라서 다음과 같은 형태가 됩니다.

\begin{align} S[i] &= S[i-1] + A[i] (\text{if } S[i-1] > 0) \\ &= A[i] \end{align}

와 같은 형태로 나타낼 수 있습니다. 이를 이용해서, S 중에서 가장 큰 값을 찾으면, 그것이 답이 됩니다. 여기서 S가 cache와 같은 역할입니다.

관련 유형 : 11053, 2225

3. Problem의 Subproblem과 다른 Subproblem이 연계되는 유형

A= operate(sub A, sub B), B = operate(sub A, sub B)와 같은 형태로 나타나는 경우를 말합니다. 이와 같은 유형은 두 개 이상의 subproblem이 서로 연계되기 때문에 이들을 동시에 연산하면서, 진행해야 합니다. 일반적으로는 이중 배열을 이용해서 수행하는 것이 일반적입니다. 이런 내용들을 대게 문제에서 제약사항이 있는 문제에 많이 사용됩니다. 예제를 보면 쉽게 이해가 됩니다.

백준 2133

2133번: 타일 채우기

앞 서 풀었던 2xn 타일 문제와 똑같지만, 3xn으로 바뀌었을 뿐이다. 이번에도, 앞에서 부터 한 번씩 경우의 수를 따져보는 것이 중요하다. 먼저 세로를 넣은 경우에는 아래에 가로가 하나 강제되는 것을 볼 수 있다. 그리고, 가로로 넣은 경우에는 세로로 세우거나 가로로 세우는 것을 볼 수 있다. 따라서, 3가지의 경우의 수로 볼 수 있다. 하지만, 우리가 구하고자 하는 모양과는 다른 모양의 조각이 남는 것을 볼 수 있다. 따라서, 우리가 구하고자 하는 것(3xn을 채우는 경우의 수)을 cache[n][0]이라 하고, 그를 위해 부가적으로 해결해야 하는 문제(밑변이 n이고, 윗변은 n-1, 좌는 2, 우는 3인 도형을 채우는 경우의 수)를 cache[n][1]이라고 하자.

그렇게 하면 아래와 같은 점화식을 얻을 수 있다.

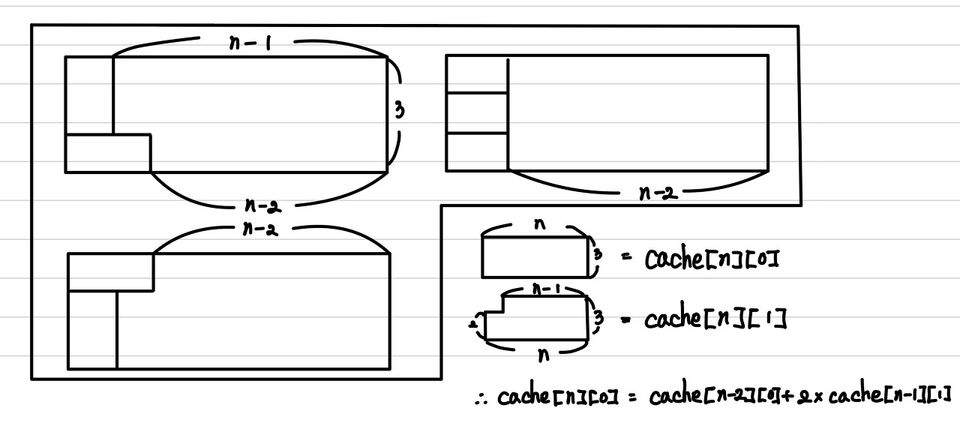
tile_3_1

하지만, 다른 부가적인 문제에 대한 점화식을 세우지 못했기 때문에, 이에 대한 점화식도 찾아주어야 한다. 왼쪽에 세로를 채우게 되는 경우와 가로를 바로 채우는 경우가 있을 것이다. 해당하는 경우는 각 각 다음과 같이 묘사되고, 점화식도 동일하게 얻을 수 있다.

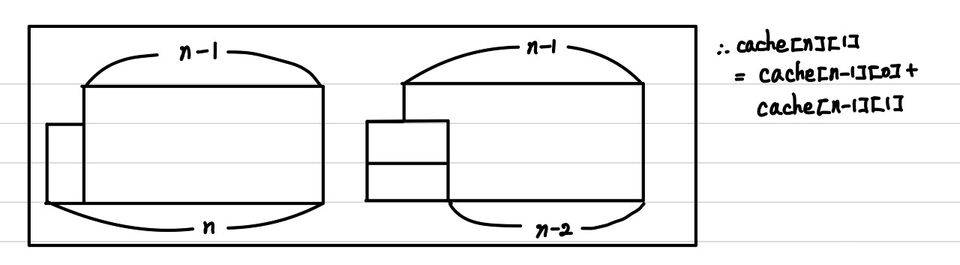
tile_3_2

이제 이를 반복해서 풀어나가면 쉽게 답을 구할 수 있다.

이런 식으로 하나의 subproblem을 풀기 위해서 연계되는 subproblem이 생기는 유형도 존재한다.

관련 유형 : 11054, 13398, 1309, 2156, 1149

4. 동적계획법을 통해서 얻은 결과값을 추적하는 유형

해당 유형은 상당히 간단하게도 parent라는 별도의 list를 만들어서 구현할 수 있다. 즉, cache의 값을 갱신해줄 때 영향을 준 subproblem의 index를 저장해두는 것이다. 이를 통해서 해당 값이 어디서부터 유래되었는지를 후에 추적하는 것이 가능하다.

백준 14002

[14002번: 가장 긴 증가하는 부분 수열 4

수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이

www.acmicpc.net](https://www.acmicpc.net/problem/14002)

유형 2와 동일한 풀이로 풀 수 있는 문제이다. 만약, cache값을 수정하는 연산이 발생하면, parent를 변경하면 된다.

위에 언급한 모든 풀이는 해당 Github에 존재합니다.

GitHub - euidong/BOJ: 백준 알고리즘 문제 풀이