[Bitcoin] 1. ECDSA를 이용한 서명

Intro

Blockchain을 공부하게 되었는데, 이번 기회에 제대로 하자는 생각에서 Bitcoin 구현을 직접 수행해볼 생각입니다. 학습에 사용한 책은 위에 나와있는 책을 활용하였습니다.

해당 Posting은 Bitcoin이 무엇이고, 이것으로 무엇을 할 수 있는지에 대해서 설명하지 않고 Bitcoin을 구현하는 기술에 대하여 다룹니다. 또한, 책의 모든 내용을 충실히 번역하는 것이 아닌 작성자의 생각이 많이 담겨 있으니 유의 바랍니다.

해당 chapter에서는 데이터의 인증을 어떻게 수행할 것인가에 대한 세부적인 내용을 다루겠습니다.

(+) 들어가기에 앞 서...

Bitcoin에서는 결제가 발생할 때, 이전 거래에서 얻은 Bitcoin을 통해서만 결제가 가능합니다. (거래를 통해 Bitcoin을 받은 적이 없다면, Bitcoin이 없는 것으로 간주합니다.)

또한, 우리는 이 거래 내역을 모두가 볼 수 있도록 공개합니다. 이 상황에서 우리가 특정 거래 내역에서 돈을 받은 사람이 자신이고, 그 거래에서 얻은 Bitcoin을 현재 거래에 사용할 것임을 증명하기 위해서는 어떻게 해야할까요?

일반적으로 인증이라는 것은 누군가가 특정 사실을 증명하는 것을 말합니다. 여기서는, 데이터의 작성자가 진짜 작성자가 맞는지를 확인하는 것입니다. 이는 대게 믿을 만한 제3 자에게 맡기거나 직접 눈으로 확인하는 방식이 있습니다. 하지만, 매번 이를 수행하는 것은 어렵기 때문에 우리는 원본 데이터에 서명을 하는 것을 택합니다. 이를 통해서, 자신이 해당 데이터의 작성자임을 분명하게 표시할 수 있습니다. 그런데, 이것을 programming 적으로 구현하는 것은 쉬운 일이 아닙니다.

대게 이를 위해서 우리는 공개키 방식이라는 것을 사용합니다. 공개키 방식이란, 암호화하는 도구와 해독하는 도구가 서로 다른 경우를 말합니다.

즉, 해독하는 도구는 누구나에게나 제공을 하고, 암호화하는 도구는 자신만이 가지고 있도록 하여, 원본 데이터와 원본 데이터를 암호화한 데이터를 같이 보내면, 이를 받은 사용자들이 해독하는 도구를 통해 암호화한 데이터를 복구하고, 원본데이터와 대조해보면, 원본데이터의 작성자가 전송자임을 명확하게 확신할 수 있는 것입니다. 즉, 원본데이터를 암호화한 데이터가 바로 하나의 서명이 되는 것입니다. 왜냐하면, 이를 암호화하는 키는 전송한 사람만 갖고 있기 때문입니다.

programming적으로 이러한 공개키 방식을 구현하는 것은 one way function (한 방향 함수, 암호화는 쉽지만 inversion이 어려운 함수, 암호화 도구)이면서, trap door(속임수, 해독하는 도구)를 가지는 algorithm을 찾아내는 것입니다. 즉, key를 갖고 있으면 쉽게 암호를 생성할 수 있지만, key가 없다면, 이를 만드는 것이 사실상 불가능하도록 만드는 것입니다. 여기에서 일반적으로 가장 많이 사용되는 것이 RSA라는 소인수 분해의 난해함을 이용하는 algorithm이 있습니다.

하지만, Bitcoin에서는 서명을 하기 위해서, ECDSA(Elliptic Curve Digital Signature Algorithm)를 사용합니다. 따라서, 여기서는 이 기술에 대해서 자세히 알아볼 것입니다.

일단 이를 이해하기 위해서 이를 이루는 기반 수학적 용어를 먼저 배워야 합니다.

1. 유한 공간 Finite Field
2. 타원 곡선 Elliptic Curve

따라서, 이에 대한 내용을 이제부터 하나하나씩 살펴보겠습니다.

1. 유한 공간 Finite Field

들어가기에 앞 서 두 가지 개념을 정리하고 가야 합니다.

먼저, 소수입니다. 소수(Prime Number)는 1과 자신 이외의 자연수로 나눌 수 없는, 1보다 큰 자연수입니다. 또한, 해당 숫자들은 규칙성을 갖고 있지 않기 때문에, 하나의 소수가 주어진 뒤에 이보다 큰 바로 다음 소수를 찾는 것은 직접 해보지 않으면 알 수 없습니다.

다음은 modulo(나머지 연산자, %)입니다. 특정 값을 나누고, 남은 나머지를 반환하는 연산자라고 말할 수 있습니다.

$10 \% 3 = 1, 10 \% 2 = 0$

해당 연산은 일반적인 대수학의 연산과는 다르게 동작하게 하기 때문에, 이에 대하여, 앞으로 사용할 특징 몇 가지를 정리해보겠습니다.

1. $a \% b \lt b$
2. $(a \times b) \% c = \{(a \% c) \times (b \% c)\} \% c$
3. $a^{b} \% (b-1) = 1$

위의 3가지 특징에 대한 자세한 증명은 여기서 다루기보다, 궁금하시다면, 직접 찾아보시길 바랍니다.

이를 통해서 Finite Field에서의 연산을 표현할 수 있으니 이를 기억해둡시다.

Finite Field란 특정 소수보다 작은, 0을 포함한 자연수 집합으로, 이루어지고,

$F\_3 = \{ 0, 1, 2 \}$

$F\_{11} = \{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \}$

다음 6가지 조건을 만족하는 집합을 의미합니다.

• Additive closed, 덧셈에 대하여 닫혀있다.
• Multiplicative closed, 곱셈에 대하여 닫혀있다.
• Additive identity, 덧셈에 대한 항등원($0$) 을 갖는다.
• Multicative identity, 곱셈에 대한 항등원($1$) 을 갖는다.
• Additive inverse, 덧셈에 대한 역원($-a$)을 갖는다.
• Multicative inverse, 곱셈에 대한 역원($a^{-1}$)을 갖는다.

각 조건을 살펴보기에 앞서서 Finite Field를 정의하는 소수보다 큰 값은 해당 소수를 통해서 modulo 연산되어, Finite Field에 속하게 됩니다. (이는 modulo 연산의 첫 번째 특징($a \% b \lt b$)을 통해 알 수 있습니다.) 마치 시계와 같이 순환하는 구조를 가진다고 생각할 수 있습니다.

이를 통해서, Finite Field의 첫 번째와 두 번째 조건은 만족한다는 것을 알 수 있습니다. 왜냐하면, 덧셈과 곱셈으로 생성된 결괏값은 반드시 다시 Finite Field에 속하게 되기 때문입니다.

세 번째, 네 번째 조건은 소수는 항상 2보다 크기 때문에, 0과 1을 포함할 수밖에 없음을 알 수 있습니다. 따라서, Finite Field는 덧셈과 곱셈에 대한 항등원을 가진다는 것을 확인할 수 있습니다.

다섯 번째는 다음과 같습니다.

$F\_{p} = \{0,1,2,3,..., p - 2, p - 1\}$이고, $a \in F\_{p}$인 경우

$-a = p - a$

라고 정의할 수 있습니다.

여섯 번째는 다음과 같습니다.

$F\_{p} = \{0,1,2,3,..., p - 2, p - 1\}$ 이고, $a \in F\_{p}$인 경우

$a^{-1} = a^{-1} \times 1 = a^{-1} \times a^{p-1}$

$a^{-1} = a^{p - 2}$

modulo의 세 번째 특징을 활용하여 다음과 같이 정의할 수 있습니다.

이러한 modulo 연산을 활용하는 Finite Field의 특징은 다음과 같습니다.

위에서 보았듯이 덧셈과 곱셈 연산은 역원이 존재하여, 결괏값을 갖고 역으로 원래 값을 찾아내는 것이 가능합니다. 하지만, 이 공간에 역이 없는 연산자를 추가한다면 어떻게 될까요? 이를 기억하고 넘어갑시다.

2. 타원 곡선 Elliptic Curve

다음 식을 만족하는 점들이 그리는 곡선을 우리는 타원 곡선이라고 합니다.

$y^2 = x^3 + ax + b$

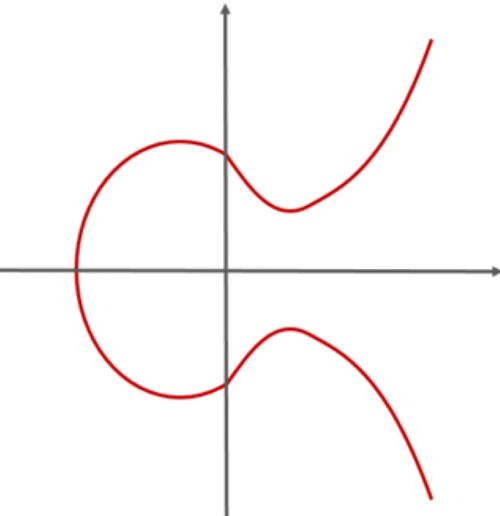
타원 곡선 상에서 우리는 덧셈 연산과 굉장히 유사한 연산을 정의할 수 있습니다. 실제로 동작은 일반적인 수학에서의 덧셈은 아니지만, 덧셈의 특징을 갖기 때문에 $+$ 기호로 표현합니다.

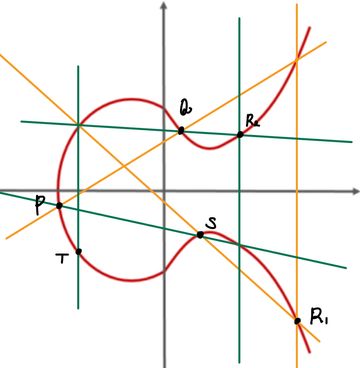
바로, 각 타원 곡선과 3개의 점을 가지는 선을 그었을 때, 항상 다음 식을 만족한다는 것입니다. (R은 타원곡선과 만나는 세 번째 점을 X축 대칭이동한 점을 말합니다.)

$P + Q = R$

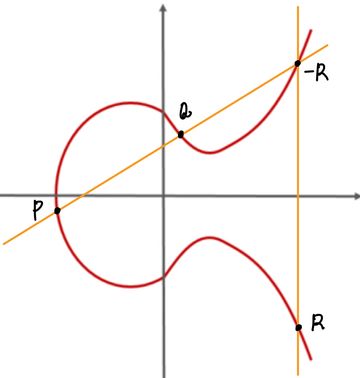
$P(x\_1, x\_2)$, $Q(x\_2, y\_2)$가 타원 곡선 $y^2=x^3 + ax + b$ 위의 점이라고 할 때, $R(x\_3, y\_3)$의 좌표는 다음과 같이 표현할 수 있습니다.

• $s = {dx \over dy} = { 3x^2 \over  2y } = { {y\_2 - y\_1} \over  {x\_2 - x\_1}}$
• $x\_3 = s^2 - x\_1 -x\_2$
• $y\_3 = s(x\_1 - x\_3) - y\_1$

이 연산 역시 다음과 같은 조건을 만족시킵니다.

• Identity, 항등원이 존재한다. => $A + I = A$
• Invertibility, 역원이 존재한다. => $A = (a\_1, a\_2)이면, -A= (a\_1, -a\_2)$
• Commutativity, 교환 법칙 => $A + B = B + A$
• Associativity, 결합 법칙 => $A + (B + C) = (A + B) + C$

여기서의 역원은 x축 대칭 이동을 통해 얻은 값이라는 것을 확인할 수 있습니다. 또한, 교점이 세 개인 시점에서 직선의 기울기를 무한대로 계속 올리다 보면 결국은 y축에 대칭인 형태로 직선이 만들어지는 것을 볼 수 있습니다. (아래 그림에서 두 번째) 이 경우에 우리는 실제로는 교점이 두 개지만, 무한대 지점에서 교점이 하나 더 있다고 말하고 이를 I(Infinity)라고 정의합니다. 그렇게 되면, 항등원이 바로 I가 되는 것을 확인할 수 있습니다. (두 번째 그림에서 $P + I = P$가 되는 것을 확인할 수 있습니다.) 이를 통해서 두 번째에 존재하는 역원까지도 증명이 가능합니다.($P + (-P) = I$)

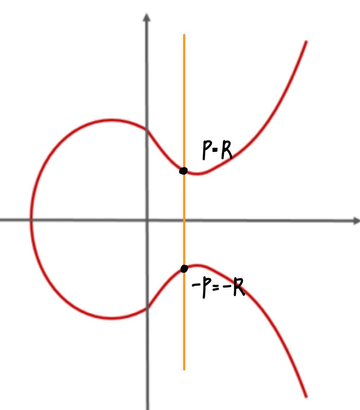
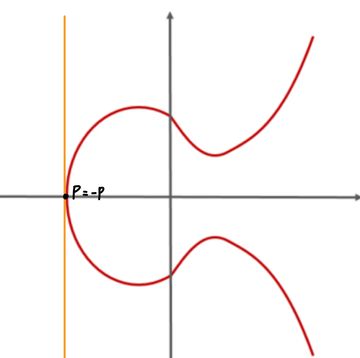
세 번째는 너무나 자명하기 때문에 넘어가고, 네 번째는 아래 그림을 통해서 설명할 수 있습니다.

주황색 : $(P + Q) + S = R\_1 + S = T$

초록색 : $(P + S) + Q = R\_2 + Q = T$

추가적으로 살펴볼 수 있는 하나의 연산을 하나 더 알아보고 갑시다.

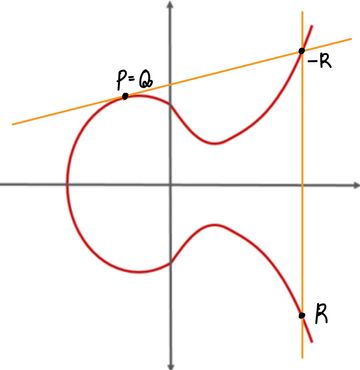
바로 접선에서 연산입니다. 이 경우는 P와 Q가 같다고 여깁니다. 즉, 자기 자신을 두 번 더 하는 것과 같습니다. 따라서, 우리는 이를 $P + P = R = 2P$라고 표현합니다. 또한, 이를 반복하면서, 결과 값을 도출할 수 있습니다. 따라서, 우리는 다음과 같은 식도 작성이 가능합니다. (이를 우리는 Elliptic Curve에서의 Scalar Multiplication이라고 합니다.)

$kP = R$

이를 계산하기 위해서는, 일반적으로 k 번의 Elliptic Curve Addition을 수행하게 됩니다. 하지만, 이를 더 간략화할 수 있는 방법이 있습니다.

$R = 63P = (1 + 2 + 4 + 8 + 16 + 32) P = (1 + (1+1) + (2+2) + (4+4) + (8+8) + (16+16)) P$

즉, 이전 계산의 결과를 현재 계산에 활용하여 계산을 더 빠르게 할 수 있습니다. 위 예시에서는 62(63 - 1) 번의 더하기 연산을 10번으로 줄인 것을 볼 수 있습니다. (물론 이외에도 많은 방식으로 최적화를 할 수 있지만, 이 정도면 대게 충분합니다.)

여기서 주목할 포인트를 하나 짚어보고 가야합니다. 우리가 $R$과, $P$를 알고 있을 때, $k$ 구하는 것이 가능할까요?

이는 쉽지 않은 문제가 됩니다. 왜냐하면, 이러한 scalar multiplcation문제에서는 역원이 존재하지 않기 때문에, k에 값을 1부터 대입해보면서 확인해 볼 수밖에 없습니다.

이제 기본이 되는 두 이론을 세팅하였습니다.

일단은 유의해야 할 점은 바로 Finite Field로 Elliptic Curve를 가져오게 되면, 이는 discrete(불연속) 해진다는 점입니다. 또한, Scalar Multiplication에도 변화가 발생합니다. 바로 순환이라는 것이 생긴다는 점입니다. $nP = R = 0$ 이 되는 $n$값이 존재하게 된다는 것입니다. 또한, 역원이 없는 성질 또한 유지되기 때문에, $kP$를 통해서 생성된 값($R$)과 P를 모두 공개하더라도, $k$가 밝혀질 가능성은 $n$값이 커질수록 불가능에 가깝다는 것입니다.

실제로 Bitcoin에서는 이 N을 매우 크게 설정하였기 때문에 문제가 없다고 할 수 있습니다. 한 번 Bitcoin에서, Finite Field 상의 Elliptic Curve의 모든 변수를 정리해봅시다.

기본적으로, 해당 암호화에 사용되는 모든 값의 단위는 256 bits 즉, 32 bytes를 사용합니다.

1. Elliptic Curve의 형태 : $a=0$, $b=7$을 사용하는 secp256k 1을 사용합니다. 이 형태는 다음과 같습니다. $y^2 = x^3 + 7$
2. Finite Field의 소수 : 위에서 말한 대로 $n$의 값을 크게 하기 위해서 finite field 자체의 크기도 매우 커져야 하기 때문에, $p$ 역시 매우 큽니다. $p = 2^{256} - 2^{32} - 977$
3. Scalar Multiplication에 사용되는 Elliptic Curve 위의 한 점($G$) : 이 또한 매우 크기 때문에 각 좌표별로 따로 적겠습니다. $G\_x =$ 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
   $G\_y =$ 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
4. Scalar Mutiplication에 의해서 만들어지는 $k$의 범위 ($n$) : 위에서도 보았겠지만, 0x는 16진수를 의미합니다.
   $n =$ 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141

위의 데이터를 보다시피 매우 큰 범위의 값을 사용하는 것을 알 수 있습니다.

여기서 한 번 우리가 암호화 키와 해독 키(공개키)를 각 각 만들어보도록 하겠습니다.

먼저, 암호화 키($e$)를 만드는 것은 매우 쉽습니다.

바로 $n$보다 작은 임의의 수를 고르면 됩니다.

그리고, 이를 이용해서, 우리는 바로 해독 키인 공개키를($P$) 만들 수 있습니다.

$P = eG$

이렇게 하면 끝입니다. 우리는 $e$를 모르기 때문에, $P$와 $G$가 모두가 아는 값이라고 할지라도 $e$를 알아낼 수 없습니다.

그렇기에 우리는 안심하고, P를 공개할 수 있는 것입니다.

이제 우리는 이것을 이용해서 한 번 서명을 통한 인증을 수행해보도록 하겠습니다.

먼저, 우리가 보내고자 하는 데이터를 $m$이라고 하겠습니다. 하지만, 이를 바로 사용하는 것은 쉽지 않습니다. 왜냐하면, 보내고자 하는 데이터의 크기가 32 bytes를 항상 만족하지 않기 때문입니다. 그렇다면, 이를 32 bytes로 변환해줄 방법이 필요할 것입니다. 그래서, 우리는 hashing을 수행합니다. 또한, 원본데이터 자체를 알아볼 수 없게 바꿔버리는 역할도 해서 암호화의 역할도 할 수 있습니다. 이를 통해서 만들어진 데이터를 우리는 $z$라고 하겠습니다.

이제 여기서, 우리는 비밀키가 아닌 또 하나의 값을 하나 생성해야 합니다. 바로 $k$입니다. 이는 비밀키와 마찬가지로 $n$보다 작은 32bytes로 지정해야 합니다.

$kG = R$

을 전송자 측에서 계산을 하고, $R$의 $x$ 좌표를 $r$이라고 정의하면 거의 모든 설정은 끝났다고 할 수 있습니다.

이제 진짜로 서명을 시작할 수 있습니다.

바로 $uG + vP = kP = R$라고 할 때,

$u + ve = k$

$u = z / s$

$v = r / s$

가 되도록 하는 것입니다.

이렇게 되면, $u$라는 값은 $z$를 가지므로, 원본 데이터를 포함한다고 할 수 있습니다. 또한, $v$는 $r$을 포함하기 때문에 결과 값 자체를 포함하고 있다고 볼 수 있습니다.

이는 해당 방정식을 풀어서 보면, $s = ( z + re ) / k$라는 것을 알 수 있습니다. 여기서 $e$와 $k$라는 감춰져야만 하는 값이 두 개 포함되는 것을 알 수 있습니다. 해당 방정식은 안전하게도 $e$, $k$가 모두 변수로 남기 때문에 $s$, $z$, $r$을 안다고 해도 $e$와 $k$를 구할 수는 없습니다.

따라서, $s$와 $r$을 하나로 합쳐서 하나의 서명(Signature)을 이루게 됩니다.

따라서, 전송자는 $z$(보낼 데이터)와 $r$, $s$(서명)를 전송함으로써, 데이터의 수신자가 직접 서명의 적절함을 확인할 수 있습니다.

수신자는 이제 받은 데이터를 통해서 다음 과정을 진행한다고 볼 수 있습니다.

1. $u$와 $v$를 생성합니다. ($u = z / s$, $v = r / s$)
2. $uG + vP$의 연산을 수행합니다.
3. 위의 결괏값을 통해서 얻은 좌표값의 x 좌표와 r 값을 비교하여 동일한지를 확인합니다.
   $uG + vP = R$
4. 이것이 동일하다면, 해당 데이터는 인증된 데이터입니다.

이것이 BitCoin에서 사용하는 서명 방식인 ECDSA입니다. 이에 대한 구현은 github에 올려 두었으니, 확인을 원하시면 체크해보시길 바랍니다.

🔗 GitHub - euidong/bitcoin

Reference

• 🔗 Programming Bitcoin
• Tumbnail : Photo by Icons8 Team on Unsplash