DFS(2)-DFS Spanning Tree

2022년 4월 23일 10시 30분

  • # DFS
  • # Graph
  • # Tree
  • # Cycle 찾기

Intro

이전에는 DFS의 기본이 되는 요소에 대해서 알아보았지만, 이제는 좀 더 심화적인 부분을 배워보고자 한다. DFS가 그래프를 순회하면서 만드는 DFS Spanning Tree에 대한 내용이다.

DFS Spanning Tree

우리는 총 4가지로 간선을 분류할 수 있습니다.

  1. Tree Edge(트리 간선)- DFS Spanning Tree에 포함된 간선
  2. Forward Edge(순방향 간선) - 해당 간선이 가르키는 정점이 DFS Spanning Tree에서 자신의 descendant(후손)에 속하는 경우
  3. Backward Edge(역방향 간선) - 해당 간선이 가르키는 정점이 DFS Spanning Tree에서 자신의 ancestor(조상)에 속하는 경우
  4. Cross Edge(교차 간선) - 해당 간선이 가르키는 정점이 후손도 조상도 아닌 sibiling(형제 또는 그들의 자손)에 속하는 경우

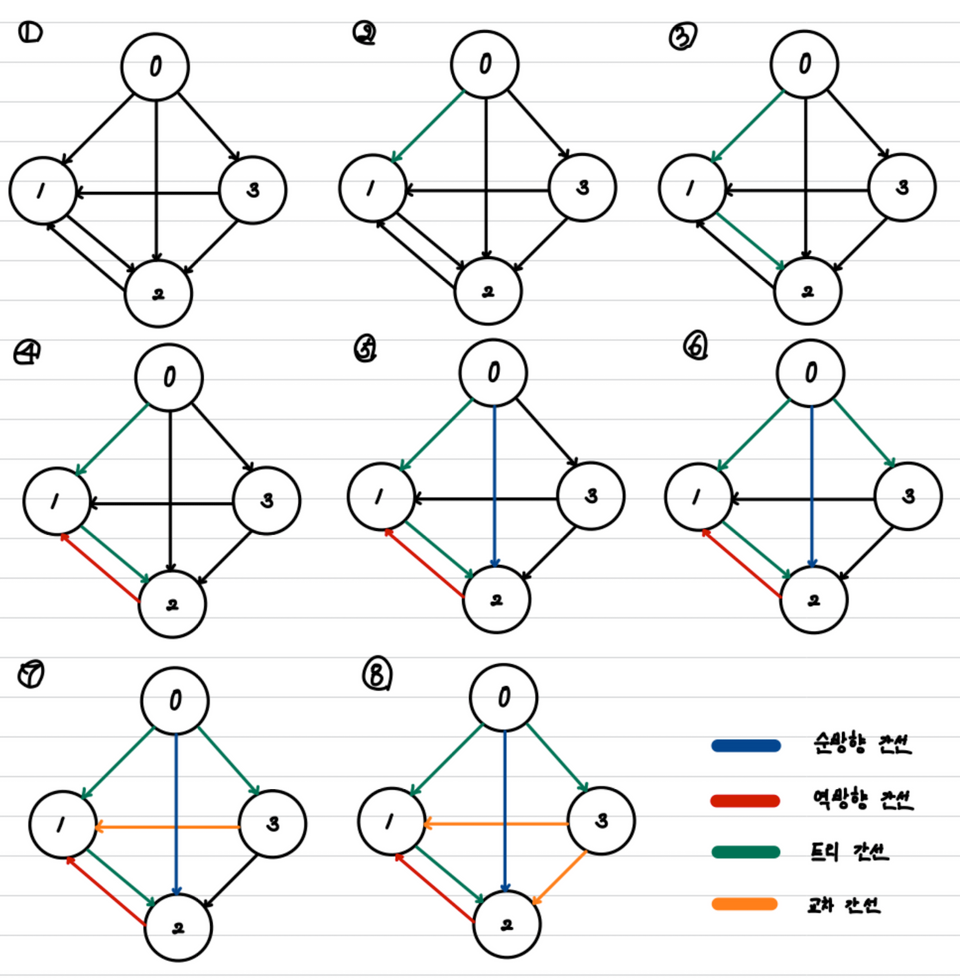
dfs-spanning-tree

이를 구현하기 위해서는 총 두 개의 추가적인 자료구조가 필요하다.

  1. order[1...N] = 해당 노드의 발견 순서
  2. finished[1...N] = 모든 간선의 사용 여부
1adj = [
2  [1,3],
3  [2],
4  [1],
5  [1,2]
6]
7N = len(adj)
8
9order = [-1] * N
10finished = [False] * N
11cnt = [0]
12def dfs(curr):
13  order[curr] = cnt[0]
14  cnt[0] += 1
15  for next in adj[curr]:
16    prefix = curr + "에서 " + next + "까지는"
17    # 아직 방문하지 않았다면, 트리 간선이다.
18    if order[next] == -1:
19      print(prefix + "트리 간선이다.")
20      dfs(next)
21    # 만약 다음 정점의 order가 더 낮다면, 순방향 간선이다.
22    elif order[next] > order[curr]:
23      print(prefix + "순방향 간선이다.")
24    # 만약, 다음 정점이 아직 거쳐야 하는 정점이 있다면, 역방향 간선이다.
25    elif not finished[next]:
26      print(prefix + "역방향 간선이다.")
27    # 그 외에는 교차 간선이다.
28    else:
29      print(prefix + "교차 간선이다.")
30  finished[curr] = True
31
32def dfsAll():
33  for i in N:
34    if order[i] == -1:
35      dfs(i)

위와 같이 구현하게 되면, 적절하게 간선을 구분할 수 있다. 위에는 방향이 존재하는 그래프였지만, 만약 방향이 존재하지 않는 무향 그래프라면 위의 과정을 좀 더 단순화할 수 있다. 먼저 간선은 다음과 같이 줄어든다.

  1. 트리 간선 = DFS Spanning Tree에 포함된 간선
  2. 중첩 간선 = DFS Spanning Tree에 포함되지 않은 간선

다음과 같이 총 2개로 줄어드는 것을 볼 수 있다. 교차 간선과 역방향 간선은 기본적으로 이후에 방문하는 정점에서 이미 방문한 정점으로 이동하는 것인데 이런 일은 무향 그래프에서는 발생하지 않기 때문에 존재할 수 없다. 그러면, 구현은 다음과 같이 진행됩니다.

1adj = [
2  [1,2,3],
3  [0,2,3],
4  [0,1,3],
5  [0,1,2]
6]
7N = len(adj)
8
9order = [-1] * N
10# finish는 필요하지 않다.
11cnt = [0]
12def dfs(curr):
13  order[curr] = cnt[0]
14  cnt[0] += 1
15  for next in adj[curr]:
16    prefix = curr + "에서 " + next + "까지는"
17    # 아직 방문하지 않았다면, 트리 간선이다.
18    if order[next] == -1:
19      print(prefix + "트리 간선이다.")
20      dfs(next)
21    # 만약 다음 정점의 order가 더 낮다면, 중첩 간선이다.
22    # 여기서 유의해야 할 점은 바로 중첩 간선은 두 번 호출된다는 점이다.
23    # 중첩 간선이기 때문에 서로 한 번씩 호출히기 때문이다.
24    # 이를 구분하기 위해서 order를 사용할 수 있다.
25    elif order[next] < order[curr]:
26      print(prefix + "order가 높은 곳에서 낮은 곳으로 가는 중첩 간선이다.")
27    else:
28      print(prefix + "order가 낮은 곳에서 높은 곳으로 가는 중첩 간선이다.")
29
30def dfsAll():
31  for i in N:
32    if order[i] == -1:
33      dfs(i)

여기서 각 간선의 특징을 이해하면, 다른 문제를 풀기 쉽다.

  1. 역방향 또는 중첩 간선의 갯수 = circle의 갯수
    • 여기서 주의할 점은 바로 무향 그래프에서는 바로 직전의 방문한 정점으로 돌아가는 정점은 매번 존재하기 때문에 이는 제외해야 한다는 것을 주의하자.
  2. 무향 그래프에서 특정 정점에서 시작되는 Spanning Tree가 중첩 간선이 없다는 것은, 해당 정점을 기준으로 연결된 정점들은 실제 그래프에서도 트리 형태로 존재한다는 점(절단점)이다.
  3. 방향 그래프에서 역방향 간선과 교차 간선이 없다면, 똑같은 의미를 가진다.

문제 풀이

DFS 문제에서는 대게 다음과 같은 자료 구조가 많이 사용한다.

  • visited : 방문 여부에 대한 checklist로, graph의 정점의 크기 만큼 존재한다. 초기 값은 False로 초기화한다.
  • order : 방문 순서에 대한 checklist로, graph의 정점의 크기 만큼 존재한다. 초기 값은 -1로 초기화하고, 방문 시마다 올려 주기 위해서, global variable로 cnt를 추가적으로 설정해주기도 한다.(그렇지 않으면, dfs parameter로 전달해주어야 한다.) 또한, 이를 통해서, visited 판단이 가능하기 때문에, 이를 사용할 시에는 visited의 사용을 하지 않아도 된다.
  • finished : 방향 그래프에서 해당 정점에 대한 탐색이 종료되었는지를 확인하기 위해서 사용되는 자료구조이며 graph의 정점의 크기 만큼 존재한다. 초기 값은 False로 초기화하고, dfs의 모든 정점을 방문하는 것이 끝난 경우에 이를 True로 세팅하자.
  • parent : 이는 대게 DFS를 재구조화할 때, 이 역시 graph의 정점의 크기 만큼 존재한다. 대게 경로를 다시 그려야 하는 경우에 많이 사용한다. 만약 visited도 같이 표현하고 싶으면, -2로 초기화하는 것이 좋다. 하지만, visited를 따로 사용할 것이라면, -1로 초기화해도 된다. 왜냐하면, parent -1은 dfs spanning tree의 root라는 의미를 가지는 값으로 쓰는 경우가 대부분이기 때문이다.

Circle 찾기

위에서 나온 대로 Circle을 찾아나가면 됩니다.

백준 16929

https://www.acmicpc.net/problem/16929

가장 기본적인 문제로 대놓고, Circle을 찾으라고 합니다. 유의할 점은 직전에 그쳐간 지점으로 돌아가는 것은 막아야 한다. 따라서, prev 값을 들고 가는 것을 추천한다.

백준 12946

https://www.acmicpc.net/problem/12946

응용 문제입니다. 처음에는 circle 찾기라는 것을 이해하기 어렵다. 하지만, 최대 색은 3이고, circle을 이루는 원소가 홀수인지 짝수인지를 찾는 문제로 받아들이면, 굉장히 쉽게 풀 수 있다.

백준 16947

https://www.acmicpc.net/problem/16947

가장 많이 응용되어지는 응용 예시입니다. DFS + BFS 기술을 사용해야 한다. 먼저, DFS를 통해서 Circle에 속하는 원소를 찾아내고, 해당 Circle에 속하는 원소들을 queue에 넣은 후에 거기서부터 bfs로 방문하지 않은 점을 찾아나가면 된다.

Comments

Related Posts

DFS(1)-기본
DFS(1)-기본