Intro
구간 누적합을 구하는 경우가 많이 발생한다. 하지만, 이를 저장하기 위해서 너무 많은 공간을 쓸 수는 없다. 예를 들어서 크기가 10,000인 집합에서 누적합으로 만들 수 있는 특정 수의 경우의 수를 구하고자 한다고 가정하자.
이 경우에 우리는 모든 누적합을 저장하기에는 공간이 너무 크다는 것을 알 수 있고, 이를 그렇다고 Brute Force하게 수행하기에도 시간이 충분하지 않을 수도 있다.
따라서, 우리는 효율적으로 누적합 정보를 저장할 수 있는 자료구조를 만들었다.
그것이 Segment Tree와 Fenwick Tree이다. 이들을 하나씩 살펴보도록 하자.
Segment Tree
이전에 tree posting에서 Tree를 표현하는 방법으로 List를 소개하였다. 여기서도 그 방식을 이용해야 하니 잘 알지 못하겠다면, 한 번 보고 오도록 하자. 👉 posting
우선 Segment Tree는 누적합을 표현하기 위한 이진 트리 형태의 자료구조이다. 이전에 트리는 데이터를 분류하기 위해 자주 사용한다고 하였는데, 이곳에서도 동일하다.
이는 트리의 leaf node가 원래 누적합을 배우고자 하는 리스트의 원소가 된다. 그리고 그 부모는 해당 원소들의 합으로 표현된다. 이렇게 하여 root는 전체 리스트의 총합이 되는 형태로 구현하는 것이다.
이러한 자료 구조를 가지게 되면 우리는 두 가지의 장점을 가질 수 있다.
- 특정 구간에서의 누적합을 굉장히 빠르게 구할 수 있다. ()
- 업데이트 시에도 깨지지 않고, 이를 빠르게 적용할 수 있다. ()
누적합 구하기 in segment
우선 해당 트리가 이미 만들어졌다는 가정하에서 어떻게 만에 누적합을 찾을 수 있는지를 확인해보자.
이는 1번째 index b에서부터 6번째 index g까지의 합을 구하는 연산이다.
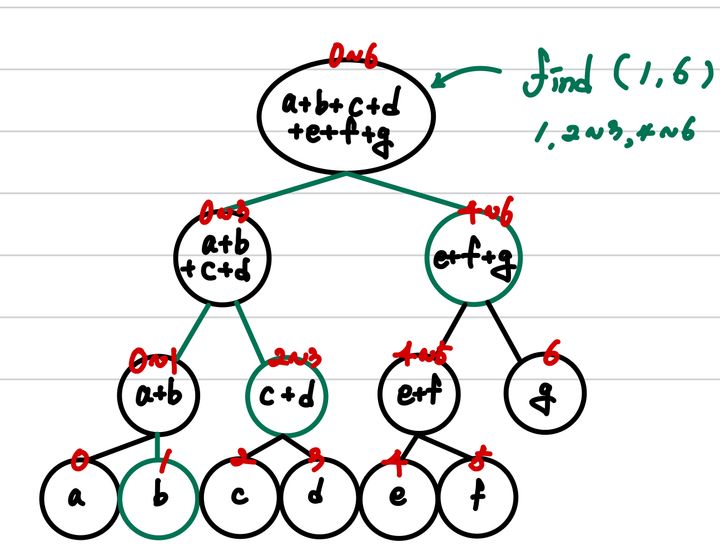
위에서 부터 탐색을 하기 위해서 다음과 같은 동작을 수행한다.
- 내가 조회하고자 하는 범위가 해당 지점이 표현하는 범위의 밖이라면, 해당 지점은 의미없으므로, 탐색을 중지한다.
- 조회 범위가 해당 지점을 완전 포함한다면, 해당값을 반환한다. (가장 큰 범위를 포함하는 지점에서부터 탐색하기 때문에 조회 범위에 엉뚱한 것이 섞이지 않는다.)
- 만약, 그렇지 않다면 해당 지점에 포함된 영역을 더 추출해야 하기 때문에 하위 지점으로 이동한다.
노드 방문 횟수가 대략 까지 감소하는 것을 볼 수 있다.
누적합 갱신 in segment
이제 실제로 update를 수행해보자.
5번째 index f에 1을 더하는 연산을 수행하는 그림이다.
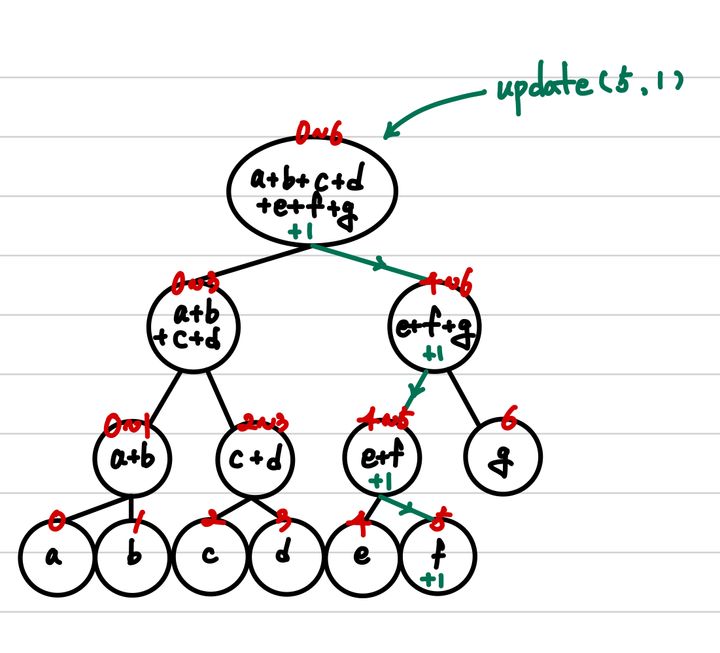
위에서 부터 변동사항을 적용하기 위해서 다음과 같은 동작을 수행한다.
- 내가 추가하고자 하는 위치가 해당 지점이 표현하는 범위의 밖이라면, 해당 지점은 의미없으므로, 탐색을 중지한다.
- 추가하고자 하는 값을 해당 지점에 추가한다.
- 해당 지점이 leaf 인지 확인하고, 맞다면 종료한다.
- 그렇지 않다면, 하위 지점을 더 탐색한다.
구현 in segment
업데이트 시에도 복잡한 연산이 없이 바로 내려가면서, 덧셈이 필요한 구역에 더해주는 것으로 쉽게 구현이 가능하다.
1S = [1,2,3,4,5,6,7] 2# tree의 크기는 원래 원래의 배열의 크기보다 큰 2의 제곱수 * 2 - 1이다. 3# 하지만, 이를 더 쉽게 만드는 방법은 간단하게 곱하기 4하는 것이다. 4tree = [0] * (len(S) * 4) 5 6# 트리를 구성하는 함수이다. 7# 루트에서부터 호출하지만, 결과는 밑에서 부터 구하면서 올라온다. 8def make_seg(start=0, end=len(S) - 1, cursor=1): 9 if start == end: 10 tree[cursor] = S[start] 11 return tree[cursor] 12 mid = (start + end) // 2 13 tree[cursor] = make_seg(start, mid, 2 * cursor) + \ 14 make_seg(mid + 1, end, 2 * cursor + 1) 15 return tree[cursor] 16 17# 위에서 보았던 누적합을 조회하는 연산이다. 18def find(left, right, cursor=1, start=0, end=len(S)-1): 19 if left > end or right < start: 20 return 0 21 if left >= start and right <= end: 22 return tree[cursor] 23 mid = (start + end) // 2 24 return find(left, right, cursor * 2, start, mid) \ 25 + find(left, right, cursor * 2 + 1, mid + 1, end) 26 27# 위에서 보았던 누적합을 업데이트 하는 연산이다. 28def update(idx, diff, cursor=1, start=0, end=len(S) - 1): 29 if idx > end or idx < start: 30 return 31 tree[cursor] += diff 32 if start == end: 33 return 34 mid = (start + end) // 2 35 update(idx, diff, start, mid) 36 update(idx, diff, mid + 1, end) 37 38make_seg() 39print(find(1, 6)) # 28 40update(3, 5) 41print(find(1, 6)) # 33
Fenwick Tree
segment tree와 동일하게 fenwick tree도 list를 통해서 tree를 표현한다. 또한, segment tree에서는 기존 배열의 시작점을 어디로 하던 상관없었지만, 구현 상의 편의를 위해서 기존 배열을 왼쪽에서 한 칸 밀어주는 것을 추천한다.
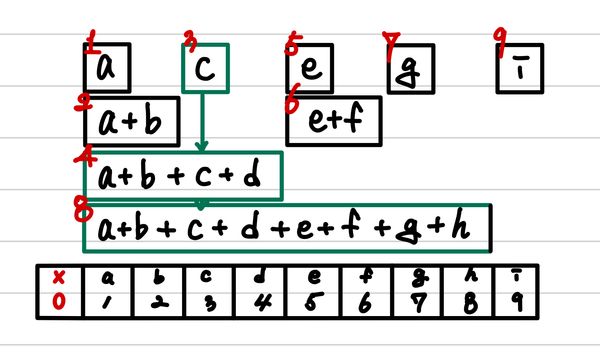
기본적으로 Fenwick Tree는 이진수의 특징을 활용한 연산을 통해서 합을 빠르게 찾을 수 있다. 먼저 Fenwick tree는 다음과 같은 형태로 구조화된다.
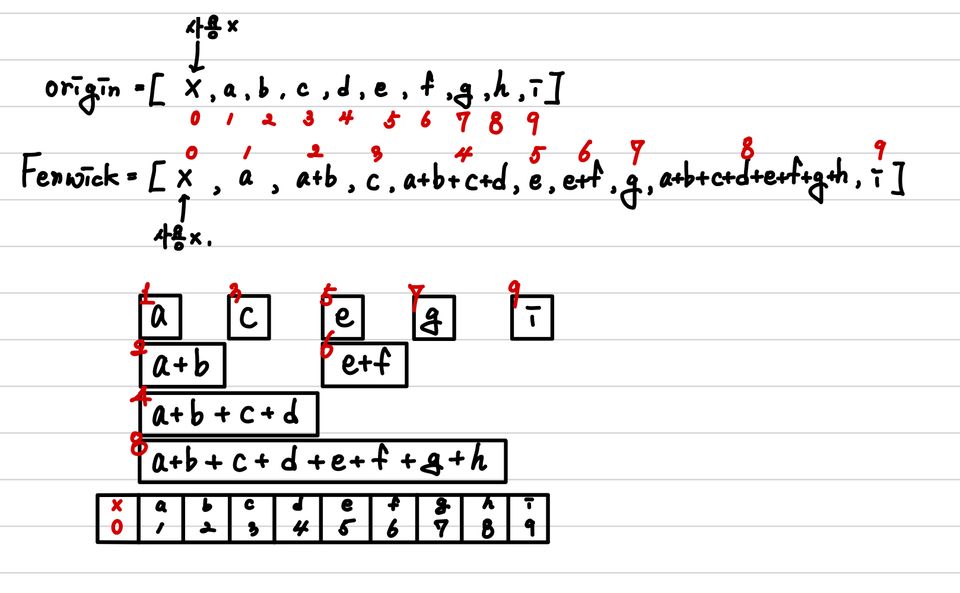
즉, 해당 수의 약수 중 가장 큰 2의 제곱 수만큼 자신을 포함한 하위 수의 누적합을 포함하는 방식이다. 따라서, 홀수의 경우는 자신만을 누적합으로 가지는 것을 볼 수 있다. 이렇게 구조화된 데이터는 LSB(Least Significant Bit, 이진수에서 가장 오른쪽에 있는 bit를 의미한다.)라는 특징을 이용해서 누적합과 해당 원소를 포함한 대상들을 찾기에 유용하다.
누적합 구하기 in Fenwick
우선 Fenwick Tree는 구간합을 반드시 맨 처음부터 특정 위치까지 구하는 연산만 수행가능하다. 따라서 구간이 처음부터가 아니라면, Fenwick Tree의 조회 연산을 두 번 수행하여 두 값을 빼서 구한다.
예시
- h라는 값을 조회하는 경우
- e + f + g의 구간합이 필요한 경우
여기서 sum을 구현하기 위해서 parameter로 들어온 값의 LSB에서 부터 1을 삭제하면서 진행하면 된다.
즉, 7이 들어왔다면, 이는 이진수로 이고, 오른쪽에서부터 1을 발견할 때마다 해당 값을 누적합에 축적하고, 삭제하면 된다.
- 누적합 acc를 0으로 초기화한다.
- 는 LSB가 1이다. 따라서, 누적합에 fenwick[]를 더한다.
- 에서 마지막 1을 지운다. (결과값은 )
- 는 LSB의 다음이 1이다. 따라서, 누적합에 fenwick[]를 더한다.
- 에서 마지막 1을 지운다. (결과값은 )
- 는 LSB의 다다음이 1이다. 따라서, 누적합에 fenwick[]를 더한다.
- 에서 마지막 1을 지운다. (결과값은 )
- 결과값이 0이므로 탐색을 종료한다.
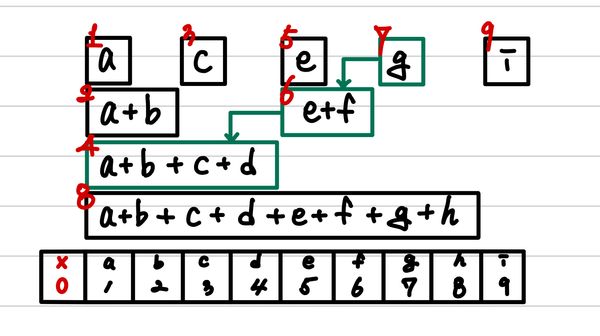
누적합 갱신 in fenwick
특정 값에 누적합을 갱신하는 것 역시 간단하게 구현이 가능하다. LSB에서 가장 가까운 1에 1을 더해주는 연산을 더해가면서 업데이트를 수행해주면 된다.
- 는 LSB가 1이다. 따라서, fenwick[]에 값을 더한다.
- 에서 가장 오른쪽의 1을 더한다. (결과값은 )
- 는 LSB의 다디음이 1이다. 따라서, fenwick[]에 값을 더한다.
- 에서 마지막 1을 더한다. (결과값은 )
- 는 LSB의 다다다음이 1이다. 따라서, 누적합에 fenwick[]에 값을 더한다.
- 더이상 더하는 것은 범위 밖이므로 종료한다.
구현 in fenwick
1origin = [None, 1,2,3,4,5,6,7,8,9] 2fenwick = [0] * len(origin) 3 4def update(idx, val): 5 while idx < len(fenwick): 6 fenwick[idx] += val 7 idx += (idx & -idx) 8 9def sum(idx): 10 acc = 0 11 while idx > 0: 12 acc += fenwick[idx] 13 idx -= (idx & -idx) 14 return acc 15 16def make_fen(origin): 17 for idx in range(1, len(origin)): 18 update(idx, origin[idx]) 19 20make_fen(origin) 21print(sum(7) - sum(4)) # 18 22update(5, 5) 23print(sum(7) - sum(4)) # 23
Versus
둘 다 구간합을 구하기에 적합한 구조이지만 다음과 같은 차이점을 가지고 있다는 점을 명시하자. 상대적으로 활용성이 높은 Segment Tree를 사용하는 것이 대다수 좋을 수 있지만, Fenwick Tree가 가지는 크기의 장점과 코드의 구현이 쉽다는 점은 굉장한 이점이다.
| Segment Tree | Fenwick Tree | |
|---|---|---|
| find 시간복잡도 | ||
| update 시간복잡도 | ||
| 공간복잡도(사이즈) | ( len(origin)) | len(origin) |
| 활용성 | 구간 내 합 뿐만 아니라 최대, 최소값으로 응용 가능 | 오직 구간 합에만 사용가능 |
| 구현 코드 길이 | 상대적으로 김 | 상대적으로 짧음 |
Comments