Tree

Intro

우리가 자료를 저장하기 위해서는 여러가지 방법이 필요하다. 그 중에서도 연관성을 가지는 데이터를 정리하는 경우에는 선형적인 list만으로는 너무나 부족할 수도 있다. 하지만, Graph를 이용하기에도 데이터의 양이 방대해지고, 규칙이 없기 때문에 원하는 데이터를 찾는 연산에서 많은 시간을 소모하게 된다.

따라서, 보다 규칙적인 형태를 가지면서, 각 지점간의 관계를 가지고, 더 안정적인 구조를 찾기 위해서 고안된 것이 트리이다.

Tree

트리(tree)란 그래프의 일종으로, 하나의 정점(root) 자체를 의미하거나 또 다른 독립된 (sub)트리를 directed edge(방향 간선)를 이용해서 연결한 자료구조를 말한다.

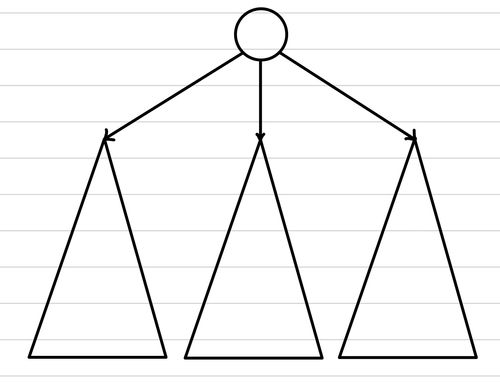
언뜻 보기에 굉장히 추상적인 표현일 수 있지만, 위와 같은 재귀적 정의를 기억하는 것도 많은 도움이 된다.

이를 좀 더 쉽게 설명하자면, 기본적으로 트리는 방향을 가진 간선으로 이루어진 그래프에서 다음과 같은 요소를 가지고 있을 경우를 트리라고 말한다.

1. 루트(root)라는 다른 정점을 가진다.
2. 루트를 제외한 모든 정점은 해당 정점으로 가는 간선(edge)이 단 하나이다.
3. 그렇기에 루트에서 모든 정점으로 연결되는 간선들의 경우의 수도 단 하나이다.

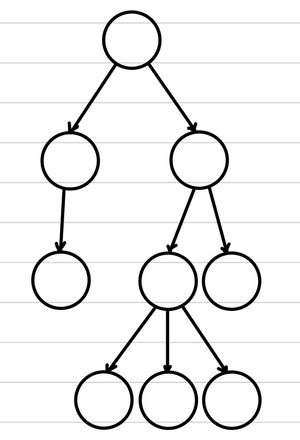
이를 이해했다면, 앞 서 살펴보았던 재귀적 정의도 이해가 되었는지 다시 한 번 확인하고 가자.

위와 같이 트리에서 루트에 연결된 서브 트리는 마치 하나의 독립적인 바구니라고 볼 수도 있다. 트리에서는 연결된 subtree가 서로 독립적이기 때문에, 독립적인 바구니에 담는 규칙을 마음대로 정하여 독립적인 특징이 있는 데이터를 분류하기에 적절한 구조를 가지고 있다.

용어

• 깊이(depth) : 트리의 최대 높이를 의미한다. 대게 루트의 높이를 0으로 보기 때문에 노드가 2개라면, 깊이가 1인 걸로 본다. 하지만, 이는 구현자의 마음에 따라 다르게 구현할 수 있다.
• 부모(parent) : 특정 정점을 기준으로 자신을 가르키는 간선을 가진 정점을 말한다. 즉, 트리의 구조에서 상위에 있는 노드라고 할 수 있다.
• 자식(child) : 특정 정점을 기준으로 자신에서 출발하는 간선에 연결된 정점을 말한다. 즉, 트리의 구조에서 하위에 있는 노드라고 할 수 있다.
• 조상(ancestor) : 특정 정점을 기준으로 자신으로 오는 경로가 존재하는 정점을 말한다. 즉, 트리의 구조에서 부모에서 부터 루트까지에 경로의 모든 노드가 이에 포함된다.
• 루트(root) : 부모가 없는 최상단의 정점을 의미한다.
• 리프(leaf) : 자식이 없는 최하단의 정점들을 의미한다.
• 서브트리(subtree) : 트리의 각 정점은 해당 정점을 루트로 하는 트리라고 볼 수 있다. 이러한 본래 트리에 존재하는 내부 트리를 서브트리라고 한다.

Binary Tree

모든 정점의 자식의 크기가 2 이하로 정해진 트리를 이진 트리(Binary Tree)라고 한다.

• Skewed Binary Tree
  이진 트리에서 같은 depth에 있는 정점이 단 하나 밖에 없는 경우를 말한다. 마치 Linked List와 같은 형태이다. 이는 트리의 목적 중 하나인 분류라는 기능을 적절히 수행하지 못하는 형태이기 때문에 대게 좋지 않은 형태로 본다.

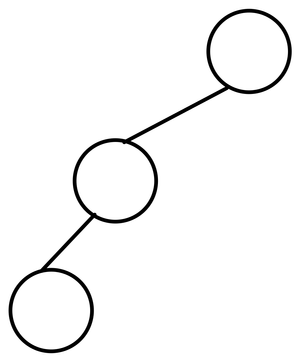
• Balanced Binary Tree
  균형 잡힌 이진 트리로 좌우의 depth가 최대 1까지만 차이가 나는 경우를 의미한다.

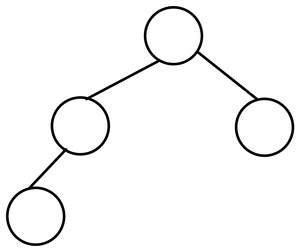
• Full Binary Tree
  정점이 가질 수 있는 자식의 수가 0 아니면 2로 제한되는 형태의 이진 트리를 의미한다. 그렇기에 기본적으로 균형 잡힌 형태의 트리가 생길 수 밖에 없다.

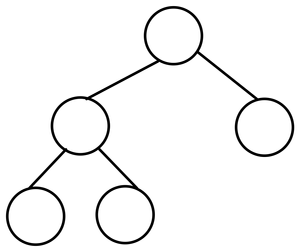
• Complete Binary Tree
  균형잡힌 트리이면서 정점이 반드시 왼쪽부터 채워지는 트리를 말한다. 해당 트리의 가장 큰 특징은 이를 Array로 표현하기에 최적화되어있다는 점이다. 이는 후에 있을 구현법 파트에서 더 자세히 알아본다. 따라서, Complete Tree를 기억하고 가자.

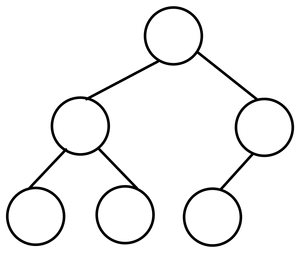
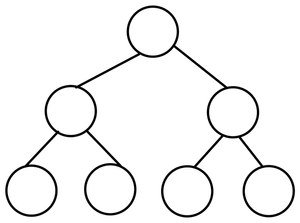
• Perfect Binary Tree
  Complete Tree와 가장 혼돈되는 개념이다. 이는 모든 이진 트리가 빈틈없이 꽉 채워진 경우를 말한다. 즉, leaf 노드의 자식의 갯수가 모두 0일 때이다.

속성

해당 속성은 정의에 의해서 파생되는 내용이다. 직접 상상해서 왜 안되는지를 생각해보자.

• 루트에 연결된 subtree 간에는 간선이 존재하지 않는다.
• Cycle이 존재하지 않기 때문에, Graph의 종류 중 하나인 DAG에 속한다.
• 정점과 정점 사이의 경로가 있다면, 해당 경로는 유일한 경로이다.
• 형제 노드로 이동할 수 있는 방법은 존재하지 않는다.

구현법

트리는 표현하기 위해서 대표적으로 두 가지를 사용한다. 리스트를 이용한 구현 방법과 구조체(or Class)를 이용한 구현이다.

1. 구조체

일반적으로 가장 널리 사용하는 방법이다. 먼저 Tree라는 구조체(or Class)를 정의한다.

1class Tree:
2  def __init__(self, value, subtrees):
3    self.root = value
4    self.subtrees = subtrees
5    # 필요에 따라서, 부모의 정보가 필요한 경우에는 parent를 저장할 수도 있다.

이진 트리에 경우에는 단 두 개의 subtree로 정해져있기 때문에 아래와 같은 형태를 빈번히 사용한다.

1class Tree:
2  def __init__(self, value, left, right):
3    self.root = value
4    self.left = left
5    self.right = right

이를 통해서 각 Tree type의 변수는 모두 루트 값과 subtree들을 포함하게 된다.

2. 리스트

트리의 각 정점의 유일한 특징을 이용하여 표현한다. depth와 왼쪽에서부터 몇 번째 인지를 나타내는 index를 같이 사용하면, 정점의 위치를 특정하여 표현할 수 있다. 따라서, 다음과 같은 식으로 Tree의 정점을 표현하는 것이다.

만약, 이진 트리와 같은 경우에는 아래와 같은 식으로 해당 노드가 어느 곳에 존재하는지를 찾을 수 있다.

1. $\text{tree}[2^{i} + j] =$ depth가 i이고, 왼쪽에서 j만큼 떨어진 정점이 지닌 값
2. $\text{tree}[i]$의 자식은 $\text{tree}[i \times 2]$ 또는 $\text{tree}[i \times 2 + 1]$이다.

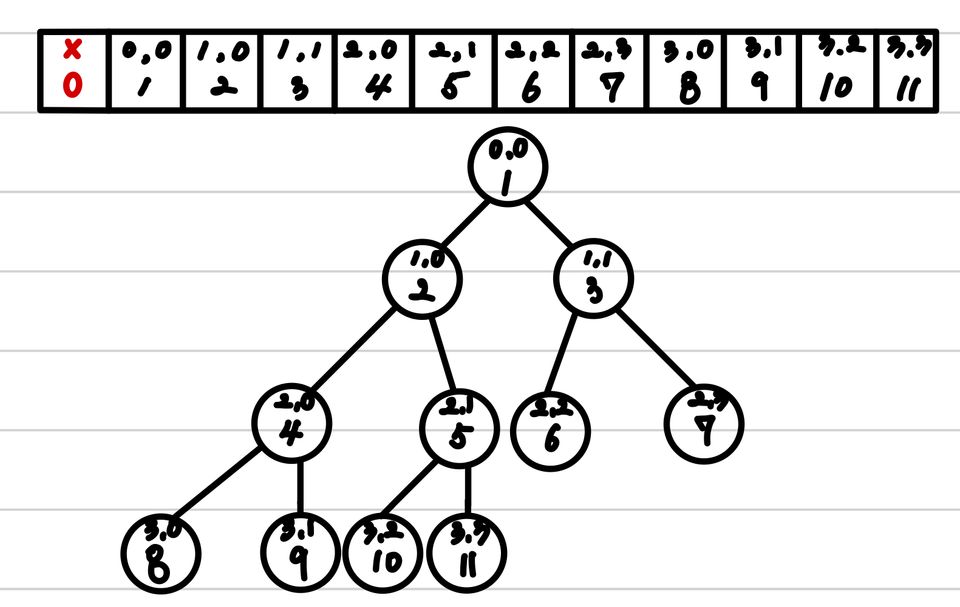
이때 반드시 주의할 점은 시작 점은 0이 아니라 1이 되도록 해야한다는 점입니다.

이는 트리의 노드의 수가 제한되어 있는 경우에만 사용할 수 있으며, 효율적으로 사용하기 위해서는 최대한 Complete Tree형태를 갖추어야 한다. 왜냐하면, 왼쪽에서부터 데이터를 채우기 때문에 Complete Tree 형태의 구조여야지만 최대 효율을 낼 수 있는 것이다.

Binary Search Tree

검색 트리(Search Tree)란 트리를 이용해서 검색을 쉽게하기 위해서 일정한 규칙에 따라서 데이터를 저장한다. 이 방식은 해당 자료를 조회하는 과정이 굉장히 단순화 될 수 있다는 장점을 가진다. 그 중에서도 Binary Search Tree는 일정한 규칙을 데이터의 삽입 시에 현재 위치에 정점보다 데이터가 크다면 오른쪽, 작다면 왼쪽에 배치시킨다.로 정의한 경우를 말한다. 이렇게 데이터를 저장하게 되면, 마치 이진 검색을 통해서 데이터를 찾는 것과 같은 효과를 가질 수 있다. 왜냐하면, 후에 내가 데이터를 찾을 때 현재 위치의 값을 확인하고 해당 값보다 찾고자 하는 값이 크다면 반드시 오른쪽에 있을 것이라는 확신을 가질 수 있기 때문이다. 이를 통해서, 검색 범위를 줄일 수 있기 때문에 우리가 마치 이진 검색을 하는 것처럼 데이터의 범위를 한정할 수 있다. 이게 앞에서 설명했던 트리가 가지는 분류의 기능이다. 기존의 리스트에서는 정렬을 통해서 index 번호가 순서라는 정보를 담고 있었다면, Binary Search Tree에서는 좌우 subtree가 대소 비교라는 정보를 갖고 있는 것이다.

하지만, 위에서 살펴보았다시피 유의할 점은 데이터가 좌우로 골고루 퍼져 있어야 한다는 점이다. 만약, 데이터가 좌축에만 쏠려있다면(skewed), 결국에는 분류로 얻는 이득이 없어진다. 따라서, 검색 시에는 시간 복잡도가 $O(N~\log{N})$ 이다.

Skew 해결책

여기서는 Skew에 대한 자세한 해결책을 제시하지 않는다. 아래 키워드를 제시하였으니 이를 검색하여 찾아보길 권장한다. (후에 정리할 시간이 있다면, 정리하겠다.)

• 각 정점에 우선순위를 랜덤 값으로 지정하고, 각 subtree의 root는 해당 subtree에서의 랜덤 값의 총합을 우선순위로 가지게 하여 특정 트리가 데이터의 순서에 의해서 skew되는 현상을 막기 우히나 방법이 있다.(Treap)
• Tree의 Skew가 발생할 시에 rotation이라는 방법을 통해서 Skew를 해결 시키는 방법도 있다. (AVL Tree)
• 빨강과 검정이라는 이진 정보를 추가 활용하여 해결하는 방법도 있다. (Red Black Tree)

Advanced Topic

아래 설명된 Tree에 대한 정보는 앞으로 차근차근 포스팅할 계획이다.

• DFS Tree
• Segment Tree
• Fenwick Tree
• Heap