Intro
이전까지 특정 word를 기반으로 하여 modeling을 수행하는 방법을 알아보았다. 하지만, 우리가 특정 word의 sequence를 통해서 각 word에 대한 classification을 한 번에 하고 싶은 경우는 어떻게 할까?(예를 들어, 각 단어의 품사를 지정하는 일) 일반적으로 각 단어가 특정 해당 class일 확률로 구하는 방법이 일반적일 것이다. 하지만, 문맥을 고려하여 확률을 구할 방법은 없을까? 그 방법은 바로 bigram을 이용하면 될 것이다. 그렇다면, 사실 우리가 사용하는 문맥이 단어 자체보다는 이전 class가 더 영향이 크다면, 이는 어떻게 해야할까? 이를 위한 해결책이 HMM이다. NLP 뿐만 아니라 여러 분야에서 넓게 사용되고 있지만, 여기서는 NLP 분야에서 어떻게 이를 사용하는지를 알아볼 것이다.
Markov Model
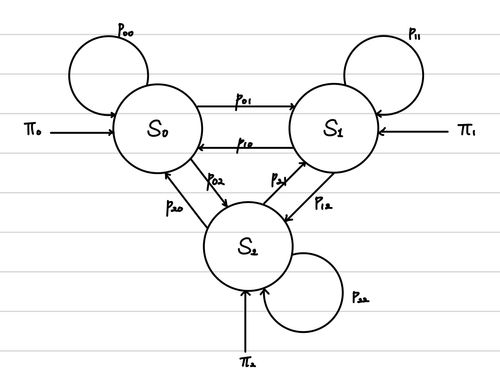
HMM을 알아보기전에 Markov Model을 알아야 한다. 이는 특정 sequence의 확률을 추정하는 방법이다. 즉 우리에게 state sequence (S = s 0 , s 1 , . . . , s N S= {s_{0}, s_{1}, ..., s_{N}} S = s 0 , s 1 , ... , s N
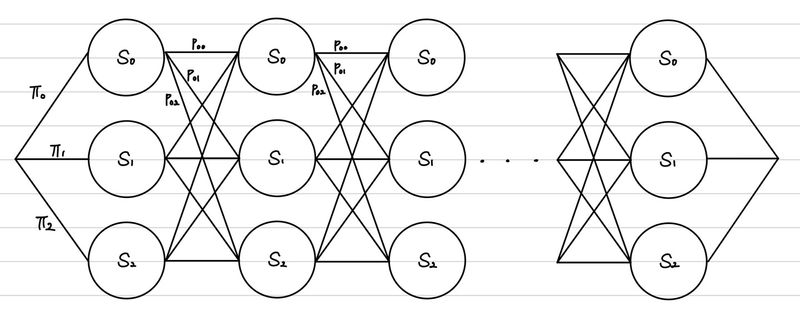
위의 그림이 state 각 각에서 다음 state로 전이할 확률을 나타낸 것이라면, 우리는 아래 그림과 같은 그림으로 sequence의 확률을 추론할 수 있는 것이다.
따라서, 위의 그림에서 우리가 만약 ( s 0 , s 1 , s 0 , s 2 ) (s_{0}, s_{1}, s_{0}, s_{2}) ( s 0 , s 1 , s 0 , s 2 )
p ( s 0 , s 1 , s 0 , s 2 ) = p ( s 0 ∣ start ) × p ( s 1 ∣ s 0 ) × p ( s 0 ∣ s 1 ) × p ( s 2 ∣ s 1 ) × p ( e n d ∣ s 2 ) = π 0 × p 01 × p 10 × p 12 × 1 \begin{align*}
p(s_{0}, s_{1}, s_{0}, s_{2}) &= p(s_{0}| \text{start}) \times p(s_{1}|s_{0}) \times p(s_{0}|s_{1}) \times p(s_{2}|s_{1}) \times p(end|s_{2}) \\
&= \pi_{0} \times p_{01} \times p_{10} \times p_{12} \times 1
\end{align*} p ( s 0 , s 1 , s 0 , s 2 ) = p ( s 0 ∣ start ) × p ( s 1 ∣ s 0 ) × p ( s 0 ∣ s 1 ) × p ( s 2 ∣ s 1 ) × p ( e n d ∣ s 2 ) = π 0 × p 01 × p 10 × p 12 × 1 이를 잘 살펴보니 bigram에서의 Likelihood를 구하는 공식과 똑같다. 즉, state 각 각을 word라고 본다면, Markov Model을 통해서 구할 수 있는 확률은 bigram의 Likelihood인 것이다.
그리고 이를 일반화하면 다음과 같다.
p ( s e q ) = ∏ i = 1 N p ( s e q i ∣ s e q i − 1 ) p(seq) = \prod_{i=1}^{N}p(seq_{i}|seq_{i-1}) p ( se q ) = i = 1 ∏ N p ( se q i ∣ se q i − 1 ) 그런데, 여기서 n이 3 이상인 ngram을 적용하고 싶다면, 각 state를 n-1 gram으로 설정하면 된다.
X i = ( Q i − 1 , Q i ) 라면, P ( X i ∣ X i − 1 ) = P ( Q i − 1 , Q i ∣ Q i − 2 , Q i − 1 ) = P ( Q i ∣ Q i − 2 , Q i − 1 ) \begin{align*}
X_{i} &= (Q_{i-1}, Q_{i}) \text{라면, }\\
P(X_{i} | X_{i-1}) &= P(Q_{i-1}, Q_{i} | Q_{i-2}, Q_{i-1}) \\
&= P(Q_{i} | Q_{i-2}, Q_{i-1})
\end{align*} X i P ( X i ∣ X i − 1 ) = ( Q i − 1 , Q i ) 라면 , = P ( Q i − 1 , Q i ∣ Q i − 2 , Q i − 1 ) = P ( Q i ∣ Q i − 2 , Q i − 1 ) 따라서, trigram을 적용해보면 아래와 같다.
p ( ( s t a r t , w 0 ) , ( w 0 , w 1 ) , ( w 1 , w 0 ) , ( w 0 , w 2 ) ) = p ( w 0 ∣ start , start ) × p ( w 1 ∣ start , w 0 ) × p ( w 0 ∣ w 0 , w 1 ) × p ( w 2 ∣ w 1 , w 0 ) × p ( e n d ∣ w 0 , w 2 ) = π 0 × p 01 × p 10 × p 12 × 1 \begin{align*}
p((start, w_{0}), (w_{0}, w_{1}), (w_{1}, w_{0}), (w_{0}, w_{2})) &= p(w_{0}| \text{start}, \text{start}) \times p(w_{1}|\text{start}, w_{0}) \times p(w_{0}|w_{0}, w_{1}) \times p(w_{2}|w_{1}, w_{0}) \times p(end|w_{0}, w_{2}) \\
&= \pi_{0} \times p_{01} \times p_{10} \times p_{12} \times 1
\end{align*} p (( s t a r t , w 0 ) , ( w 0 , w 1 ) , ( w 1 , w 0 ) , ( w 0 , w 2 )) = p ( w 0 ∣ start , start ) × p ( w 1 ∣ start , w 0 ) × p ( w 0 ∣ w 0 , w 1 ) × p ( w 2 ∣ w 1 , w 0 ) × p ( e n d ∣ w 0 , w 2 ) = π 0 × p 01 × p 10 × p 12 × 1 Hidden Markov Model
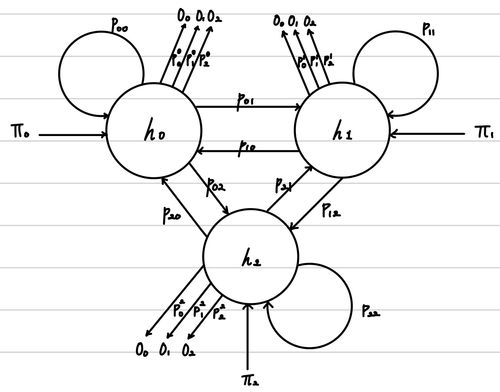
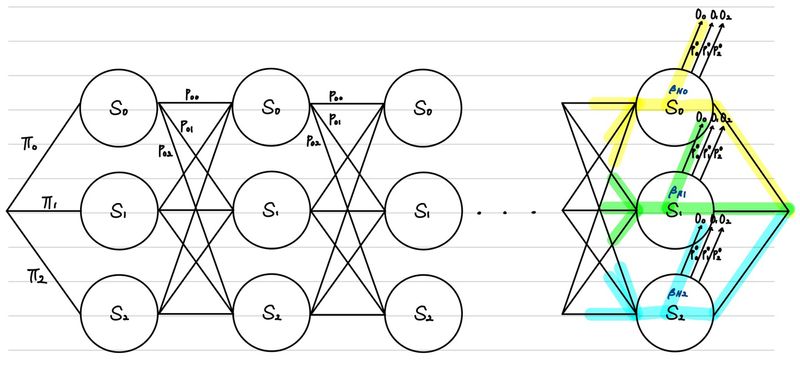
Hidden Markov Model은 state를 하나 더 만든다는 것이 핵심이다. 그래서, 우리가 직접 관측하는 state(observed state )와 직접적으로 관측하지 않지만, 관측한 state들에 의존하는 state(hidden state ) 총 두 개의 state를 사용한다. 일반적인 예시가 text가 입력되었을 때 우리는 각 단어를 observed state라고 한다면, 각 단어의 품사를 hidden state라고 정의할 수 있다.
위의 예시는 우리가 관측하는 데이터(O O O H H H
Estimation
우리가 할 수 있는 작업은 크게 두 가지이다. 일반적인 Markov Model에서 할 수 있던 방식이 Trellis 방식이고, 또 다른 방식이 Viterbi 방식이다.
( o 0 , o 1 , o 0 , o 2 ) (o_{0}, o_{1}, o_{0}, o_{2}) ( o 0 , o 1 , o 0 , o 2 ) Trellis )( o 0 , o 1 , o 0 , o 2 ) (o_{0}, o_{1}, o_{0}, o_{2}) ( o 0 , o 1 , o 0 , o 2 ) Viterbi )
위의 경우를 각각 풀어보도록 하자.
1. Trellis
우리가 직접 관측한 데이터의 sequence 자체의 확률이 궁금할 때이다. 따라서, 이에 대한 분석은 ( o 0 , o 1 , o 0 , o 2 ) (o_{0}, o_{1}, o_{0}, o_{2}) ( o 0 , o 1 , o 0 , o 2 )
p ( o 0 , o 1 , o 0 , o 2 ) = p ( o 0 , o 1 , o 0 ) × p ( o 2 ∣ o 0 , o 1 , o 0 ) = p ( o 0 , o 1 , o 0 ) × { p ( o 2 ∣ h 0 ) p ( h 0 ∣ o 0 , o 1 , o 0 ) + p ( o 2 ∣ h 1 ) p ( h 1 ∣ o 0 , o 1 , o 0 ) + p ( o 2 ∣ h 2 ) p ( h 2 ∣ o 0 , o 1 , o 0 ) } = p ( o 0 , o 1 , o 0 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = p ( o 0 , o 1 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = p ( o 0 ) × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) \begin{align*}
p(o_{0}, o_{1}, o_{0}, o_{2}) &= p(o_{0}, o_{1}, o_{0}) \times p(o_{2} | o_{0}, o_{1}, o_{0}) \\
&= p(o_{0}, o_{1}, o_{0}) \times \{p(o_{2} | h_{0})p(h_{0} | o_{0}, o_{1}, o_{0}) + p(o_{2} | h_{1})p(h_{1} | o_{0}, o_{1}, o_{0}) + p(o_{2} | h_{2})p(h_{2} | o_{0}, o_{1}, o_{0})\} \\
&= p(o_{0}, o_{1}, o_{0}) \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
&= p(o_{0}, o_{1}) \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
&= p(o_{0}) \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
&= \sum_{i=0}^{2}p(o_{0}|h_{i})p(h_{i}|start) \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) }
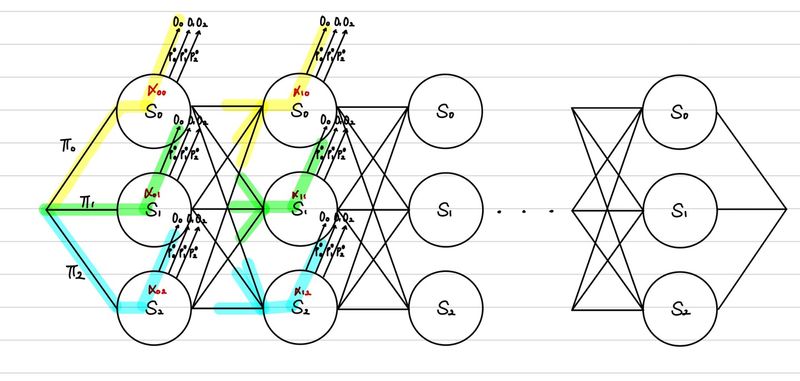
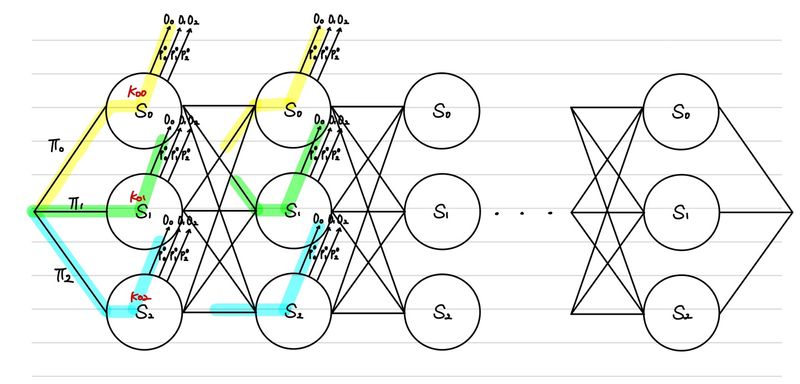
\end{align*} p ( o 0 , o 1 , o 0 , o 2 ) = p ( o 0 , o 1 , o 0 ) × p ( o 2 ∣ o 0 , o 1 , o 0 ) = p ( o 0 , o 1 , o 0 ) × { p ( o 2 ∣ h 0 ) p ( h 0 ∣ o 0 , o 1 , o 0 ) + p ( o 2 ∣ h 1 ) p ( h 1 ∣ o 0 , o 1 , o 0 ) + p ( o 2 ∣ h 2 ) p ( h 2 ∣ o 0 , o 1 , o 0 )} = p ( o 0 , o 1 , o 0 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = p ( o 0 , o 1 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = p ( o 0 ) × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) 이를 그림으로 표현하면 다음과 같다.
또한, 이 식을 다음과 같이 축소가 가능하다.
∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = ∑ i = 0 2 α 0 i × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = ∑ i = 0 2 α 1 i × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = ∑ i = 0 2 α 2 i × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = ∑ i = 0 2 α 3 i \begin{align*}
&\sum_{i=0}^{2}p(o_{0}|h_{i})p(h_{i}|start) \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
=& \sum_{i=0}^{2}\alpha_{0 i} \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
=& \sum_{i=0}^{2}{\alpha_{1 i} } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
=& \sum_{i=0}^{2}{\alpha_{2 i} } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
=& \sum_{i=0}^{2}{\alpha_{3 i} }
\end{align*} = = = = i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) i = 0 ∑ 2 α 0 i × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) i = 0 ∑ 2 α 1 i × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) i = 0 ∑ 2 α 2 i × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) i = 0 ∑ 2 α 3 i 우리는 이를 통해서, Markov Model의 특징을 하나 배울 수 있다. 그것은 바로 복잡한 sequence 전체의 확률에서 벗어나서 바로 직전의 확률값만 으로 다음 확률을 추론할 수 있다는 것이다. 이것이 Markov Chain이라는 이론이고, 이를 이용했기 때문에 Markov Model라고 부르는 것이기도 하다.
따라서, α \alpha α
α ( t , i ) = ∑ k = 1 N α ( t − 1 , k ) p ( h i ∣ h k ) p ( o = s t ∣ h i ) ( s t = input으로 들어온 sequence의 t번째 값 ) \alpha(t, i) = \sum_{k=1}^{N}{\alpha(t-1, k)p(h_{i}|h_{k})p(o = s_{t}|h_{i})} \quad (s_{t} = \text{input으로 들어온 sequence의 t번째 값}) α ( t , i ) = k = 1 ∑ N α ( t − 1 , k ) p ( h i ∣ h k ) p ( o = s t ∣ h i ) ( s t = input 으로 들어온 sequence 의 t 번째 값 ) 또, 이를 반대로 할 경우에는 다음과 같은 식을 얻을 수 있다.
∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) = ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × ∑ i = 0 2 β 3 i = ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × ∑ i = 0 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × ∑ i = 0 2 β 2 i = ∑ i = 0 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × ∑ i = 0 2 β 1 i = ∑ i = 0 2 β 0 i \begin{align*}
&\sum_{i=0}^{2}p(o_{0}|h_{i})p(h_{i}|start) \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{p(o_{2} | h_{i})p(h_{i} | o_{0}, o_{1}, o_{0}) } \\
=& \sum_{i=0}^{2}p(o_{0}|h_{i})p(h_{i}|start) \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{p(o_{0} | h_{i})p(h_{i} | o_{0}, o_{1}) } \times \sum_{i=0}^{2}{\beta_{3i}} \\
=& \sum_{i=0}^{2}p(o_{0}|h_{i})p(h_{i}|start) \times \sum_{i=0}^{2}{p(o_{1} | h_{i})p(h_{i} | o_{0}) } \times \sum_{i=0}^{2}{\beta_{2i}} \\
=& \sum_{i=0}^{2}p(o_{0}|h_{i})p(h_{i}|start) \times \sum_{i=0}^{2}{\beta_{1i}} \\
=& \sum_{i=0}^{2}{\beta_{0i}} \\
\end{align*} = = = = i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 p ( o 2 ∣ h i ) p ( h i ∣ o 0 , o 1 , o 0 ) i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ o 0 , o 1 ) × i = 0 ∑ 2 β 3 i i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × i = 0 ∑ 2 p ( o 1 ∣ h i ) p ( h i ∣ o 0 ) × i = 0 ∑ 2 β 2 i i = 0 ∑ 2 p ( o 0 ∣ h i ) p ( h i ∣ s t a r t ) × i = 0 ∑ 2 β 1 i i = 0 ∑ 2 β 0 i β ( t , i ) = ∑ k = 1 N β ( t + 1 , k ) p ( h k ∣ h i ) p ( o = s t ∣ h i ) ( s t = input으로 들어온 sequence의 t번째 값 ) \beta(t, i) = \sum_{k=1}^{N}{\beta(t+1, k)p(h_{k}|h_{i})p(o = s_{t}|h_{i})} \quad (s_{t} = \text{input으로 들어온 sequence의 t번째 값}) β ( t , i ) = k = 1 ∑ N β ( t + 1 , k ) p ( h k ∣ h i ) p ( o = s t ∣ h i ) ( s t = input 으로 들어온 sequence 의 t 번째 값 ) 위의 처럼 앞에서부터 풀이를 해나가면서, α \alpha α β \beta β
2. Viterbi
이는 observed state의 sequence에 의해서 파생되는 가장 적절한 hidden sequence를 구하는 것이 목표이다. 이를 통해서 할 수 있는 대표적인 것이 sequence classification이다.
그렇다면 가장 유력한 hidden state의 sequence를 s ^ ( H ) \hat{s}^{(H)} s ^ ( H )
s ^ ( H ) = arg max s ( H ) ∈ S ( H ) P ( s ( H ) ∣ s ( O ) ) = arg max s ( H ) ∈ S ( H ) P ( s ( O ) ∣ s ( H ) ) P ( s ( H ) ) = arg max h 1 , h 2 , . . . , h N ∈ S ( H ) P ( o 1 , o 2 , . . . , o N ∣ h 1 , h 2 , . . . , h N ) ⏟ Markov Model P ( h 1 , h 2 , . . . , h N ) ⏟ Markov Model = arg max h 1 , h 2 , . . . , h N ∈ S ( H ) ∏ i = 1 N p ( o i ∣ h i ) p ( h i ∣ h i − 1 ) \begin{align*}
\hat{s}^{(H)} &= \argmax_{s^{(H)} \in S^{(H)}}P(s^{(H)}|s^{(O)}) \\
&= \argmax_{s^{(H)} \in S^{(H)}}P(s^{(O)}|s^{(H)})P(s^{(H)}) \\
&= \argmax_{{h_{1}, h_{2}, ..., h_{N}} \in S^{(H)}}\underbrace{P(o_{1}, o_{2}, ... , o_{N}|h_{1}, h_{2}, ... , h_{N})}_{\text{Markov Model}}\underbrace{P(h_{1}, h_{2}, ... , h_{N})}_{\text{Markov Model}} \\
&= \argmax_{{h_{1}, h_{2}, ..., h_{N}} \in S^{(H)}}\prod_{i=1}^{N}p(o_{i}|h_{i})p(h_{i}|h_{i-1})
\end{align*} s ^ ( H ) = s ( H ) ∈ S ( H ) arg max P ( s ( H ) ∣ s ( O ) ) = s ( H ) ∈ S ( H ) arg max P ( s ( O ) ∣ s ( H ) ) P ( s ( H ) ) = h 1 , h 2 , ... , h N ∈ S ( H ) arg max Markov Model P ( o 1 , o 2 , ... , o N ∣ h 1 , h 2 , ... , h N ) Markov Model P ( h 1 , h 2 , ... , h N ) = h 1 , h 2 , ... , h N ∈ S ( H ) arg max i = 1 ∏ N p ( o i ∣ h i ) p ( h i ∣ h i − 1 )
즉, 각 layer에서 단 하나의 가장 큰 output만 살아남을 수 있게 되는 것이다. 이 과정이 사실상 HMM의 본질적인 목표이다. sequence를 입력해서 sequence 형태의 classification 결과를 얻는 것이다.
Modeling
여태까지 HMM을 활용하여 sequential class를 어떻게 estimation 하는지 알아보았다. 그렇다면, 이제는 이를 위해서 사용되는 확률값을 구해야한다. 필요한 확률값은 다음과 같다.
p ( h i ∣ h i − 1 ) p(h_{i}|h_{i-1}) p ( h i ∣ h i − 1 ) p ( o i ∣ h i ) p(o_{i}|h_{i}) p ( o i ∣ h i ) π i \pi_{i} π i
Trelli 방식에서 만들었던, α \alpha α β \beta β
c ( i , j , k ) = h i 에서 h j 로 넘어가고, o k 가 관측될 확률의 합 = ∑ t = 2 T α ( t − 1 , i ) p ( h j ∣ h i ) p ( o k ∣ h j ) β ( t , j ) c ( i , j ) = h i 에서 h j 로 넘어갈 확률의 합 = ∑ k = 1 K ∑ t = 2 T α ( t − 1 , i ) p ( h j ∣ h i ) p ( o k ∣ h j ) β ( t , j ) c ( i ) = h i 에서 상태를 변경하는 확률의 합 = ∑ j = 1 N ∑ k = 1 K ∑ t = 2 T α ( t − 1 , i ) p ( h j ∣ h i ) p ( o k ∣ h j ) β ( t , j ) \begin{align*}
c(i, j, k) &= h_{i}\text{에서 } h_{j}\text{로 넘어가고, } o_{k}\text{가 관측될 확률의 합} \\
&= \sum_{t=2}^{T} \alpha(t-1, i)p(h_{j}|h_{i})p(o_{k}|h_{j}) \beta(t, j) \\
\\
c(i,j) &= h_{i}\text{에서 } h_{j}\text{로 넘어갈 확률의 합} \\
&= \sum_{k=1}^{K}\sum_{t=2}^{T}{\alpha(t-1, i)p(h_{j}|h_{i})p(o_{k}|h_{j}) \beta(t, j)} \\
\\
c(i) &= h_{i}\text{에서 상태를 변경하는 확률의 합} \\
&= \sum_{j=1}^{N}\sum_{k=1}^{K}\sum_{t=2}^{T}{\alpha(t-1, i)p(h_{j}|h_{i})p(o_{k}|h_{j}) \beta(t, j)} \\
\end{align*} c ( i , j , k ) c ( i , j ) c ( i ) = h i 에서 h j 로 넘어가고 , o k 가 관측될 확률의 합 = t = 2 ∑ T α ( t − 1 , i ) p ( h j ∣ h i ) p ( o k ∣ h j ) β ( t , j ) = h i 에서 h j 로 넘어갈 확률의 합 = k = 1 ∑ K t = 2 ∑ T α ( t − 1 , i ) p ( h j ∣ h i ) p ( o k ∣ h j ) β ( t , j ) = h i 에서 상태를 변경하는 확률의 합 = j = 1 ∑ N k = 1 ∑ K t = 2 ∑ T α ( t − 1 , i ) p ( h j ∣ h i ) p ( o k ∣ h j ) β ( t , j ) 위의 값을 통해서 우리는 우리가 가지고 있던 확률을 업데이트할 수 있다.
p ( h j ∣ h i ) = c ( i , j ) c ( i ) p ( o k ∣ h i ) = c ( i , j , k ) c ( i , j ) \begin{align*}
p(h_{j}|h_{i}) &= {c(i,j)\over c(i)} \\
p(o_{k}|h_{i}) &= {c(i,j,k)\over c(i,j)}
\end{align*} p ( h j ∣ h i ) p ( o k ∣ h i ) = c ( i ) c ( i , j ) = c ( i , j ) c ( i , j , k ) 즉, 우리는 다음 과정을 수행하여 Modeling을 수행할 수 있는 것이다.
초기값 (p ( h i ∣ h i − 1 ) p(h_{i}|h_{i-1}) p ( h i ∣ h i − 1 ) p ( o i ∣ h i ) p(o_{i}|h_{i}) p ( o i ∣ h i ) π i \pi_{i} π i
Trelli를 통해서 α \alpha α β \beta β
p ( h i ∣ h i − 1 ) p(h_{i}|h_{i-1}) p ( h i ∣ h i − 1 ) p ( o i ∣ h i ) p(o_{i}|h_{i}) p ( o i ∣ h i ) p i i pi_{i} p i i 임계치에 도달할 때까지 2,3번을 반복한다.
이 과정을 대게 10번 정도만 하면 수렴하게 되고, 이를 확률로 사용하는 것이다.
Reference
Comments