Intro
컴퓨터 구조에서 기본이 되는 사칙연산과 소수의 표현방식(Floating Point)을 다룬다.
Overflow
시작하기에 앞서서 Overflow라는 개념을 알고가야한다. Overflow란 특정 변수의 표현범위를 벗어나는 경우에 발생하게 되는 에러 상황을 의미한다. 일반적인 사람의 생각에는 수의 범위가 있는 것은 이상할 수 있지만, 컴퓨터에서는 이것이 매우 당연하다. 무한대를 표현하는 것은 사실상 컴퓨터로는 불가능하다. 대신 매우 큰 수를 통해서 표현하는 것이 컴퓨터에게는 일반적이다. 예를 들어 우리가 빈번하게 사용하는 integer 변수 type은 그 값의 범위가 정해져있다. 이는 대게 하나의 변수를 표현하기 위해서 4bytes를 사용하는데 이는 32bits이기 때문에, 최대 까지가 표현의 범위가 되는 것이다. 여기에 음수를 표현하게 되는 경우에는 범위가 ~ 로 제한된다. 따라서, 이렇게 범위를 벗어나는 경우에 대해서는 programming language 마다 처리가 달라지지만, 대게 에러를 발생시키는 것이 일반적이다. (python에서는 알아서 범위를 추가한다.)
덧셈 / 뺄셈
덧셈은 각 자릿수의 합과 이전 자릿수에서 올림된 수(Carry)의 합이라고 다시 해석할 수 있다. 이진수에서는 결국 올림된 수와 두 수가 만들어 낼 수 있는 경우의 수는 00 ~ 11이다.
| A | B | Carry | Result |
|---|---|---|---|
| 0 | 0 | 0 | 00 |
| 0 | 0 | 1 | 01 |
| 0 | 1 | 0 | 01 |
| 0 | 1 | 1 | 10 |
| 1 | 0 | 0 | 01 |
| 1 | 0 | 1 | 10 |
| 1 | 1 | 0 | 10 |
| 1 | 1 | 1 | 11 |
이를 수행하기 위해서 우리는 XOR 2개와 AND 2개 그리고 OR 1개로 만들 수 있다.(C'와 S가 결과값이다.)
| A | B | Carry(C) | A XOR B(D) | A AND B(E) | C AND D(F) | E OR F(C') | C XOR D(S) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |

음수
음수는 기본적으로 2의 보수라는 방식을 활용한다. 만약 특정 수를 음수로 변환하고 싶다면 전체 수를 반전 시킨 후 +1을 수행하는 방식이다. 이를 통해서, 우리는 쉽게 음수를 생성할 수 있다. 그리고 놀랍게도 특정 수를 음수로 변환하고 덧셈을 하게 되면, 이것이 바로 뺄셈이 된다.
곱셈
먼저 이진수의 곱셈은 아래와 같이 십진수에서의 곱셈 연산과 방법은 같다.
곱해지는 수(multiplicand), 곱하는 수(multipler), 곱해진 결과(product)이다.
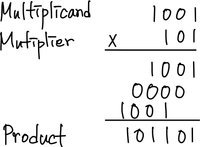
하지만, 여기서 하나의 특징을 발견할 수 있다. 각 자릿수의 결과값은 곱하는 수에 의해서 결정된다는 점이다. 곱하는 수가 1이면, 곱해지는 수의 해당 자릿수가 결과값이 되고, 0이면 무조건 0이라는 결과가 나온다는 것을 알 수 있다. 따라서, 다음과 같은 알고리즘에 따라서 연산이 수행된다는 것을 알 수 있다.
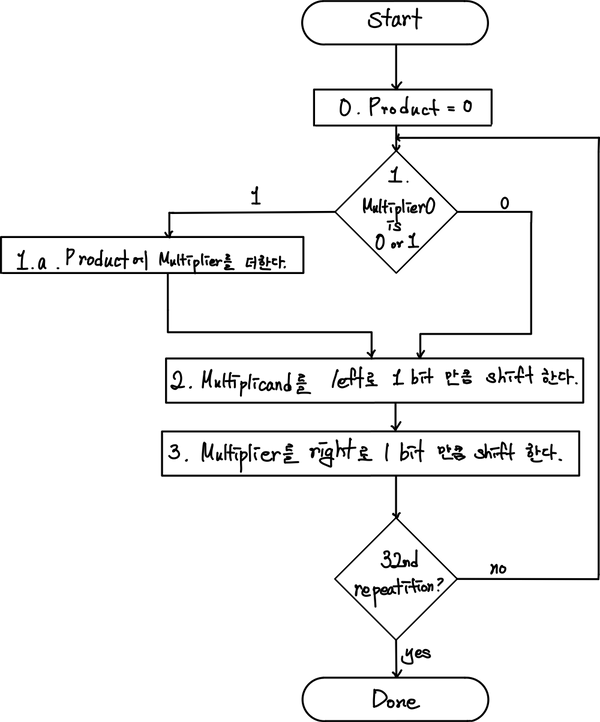
만약, 음수의 곱셈의 경우에는 간단하게 해당 값을 양수로 변환하고, 연산을 수행한 뒤에 다시 음수로 변환하는 방식을 수행한다.
나눗셈
나눗셈은 역시 동일하다.
나누어지는 수(Dividend), 나누는 수(Divisor), 몫(Quotient), 나머지(Remainder) 이다.
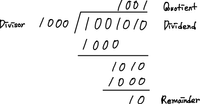
이때는 역으로 나누는 수를 오른쪽으로 32번 shift하여 매우 큰 수로 만들고, 나머지를 나누어지는 수로 초기화하여 차근차근 빼보면서 양수이면 빼고, 음수이면 되돌리기를 반복하면서 몫과 나머지를 계산할 수 있다.
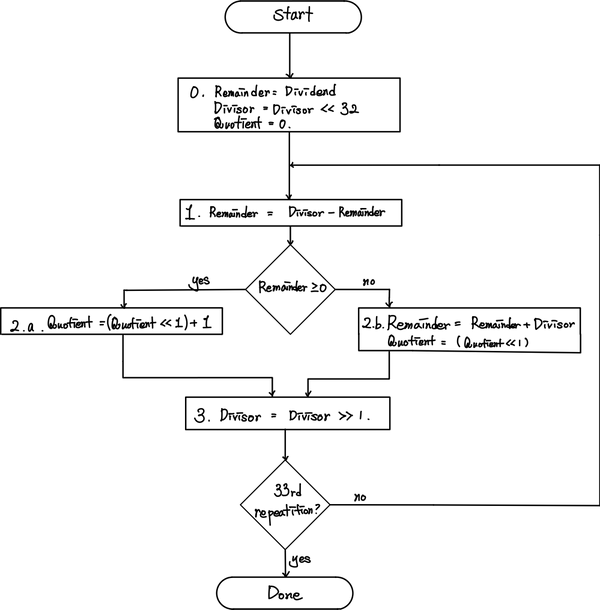
실수 연산
위에서는 여태까지 정수의 연산을 다루었지만, 소수점을 포함하는 실수 연산을 수행할 때에는 달라지는 사항이 꽤나있다.
먼저, 실수를 표기하기 위한 방법을 먼저 보자.
이를 일반적으로 normalization이라고 하며, 이진수 체계에서는 다음과 같은 형태를 갖게 된다.
따라서, 대게 실수를 표현할 때에는 x부분(fraction)과 y부분(exponent) 그리고 부호를 표현(sign)하는 부분으로 나누어서 저장한다. 이 또한, 4byte를 통해서 표현할 경우에는 x부분에 8bits, y부분에 23bits 그리고 부호에 1bit를 할당한다.
따라서, 일반적으로 표현하면 다음과 같이 쓰는 것이 일반적인 실수의 표현이다.
단, 모두 0이면 0으로 친다. floating point 연산은 후에 더 시간이 있으면 자세히 다루겠다.
Reference
- David A. Patterson, John L. Hennessy, Computer Organization and Design
- Full Adder 이미지는 WIKIPEDIA full adder의 발췌이다. (https://upload.wikimedia.org/wikipedia/commons/5/57/Fulladder.gif)
Comments