[ML] 9. Clustering

Intro

이전까지의 Posting에서는 Supervised Learning 즉, 이미 Labeling이 완료된 데이터에 의한 Learning을 중점적으로 다루었다. 지금부터는 Unsupervised Learning에 대해서 조금 더 살펴보도록 하겠다. 대표적인 Unsupervised Learning은 Clustering, Feature Selection(or Dimensionality Reduction), Generative Model 등이 존재한다. 이들에 대해서 차근차근 살펴보도록 하고, 해당 Posting에서는 가장 대표적이라고 할 수 있는 Clustering을 먼저 살펴보면서 Unsupervised Learning에 대한 계략적인 이해를 해보도록 하겠다.

Clustering

Clustering은 unlabeled data를 data간 유사성 또는 거리 지표 등을 활용하여 미리 지정한 수 만큼의 partitioning하는 작업을 의미한다. 즉, 우리가 학습을 진행함에 있어 data는 label이 존재하지 않기 때문에 우리는 data간의 관계에서 정보를 추출해서 이를 분류해내는 것이 목표인 것이다.

이를 수행하기 위한 방법은 크게 두 가지로 나눌 수 있다.

Non-Parametric Approach
이름 그대로 확률적 분포를 가정한 후, Parameter를 찾아가는 방식이 아닌 직관적인 방법(Huristic Approach)을 활용하는 방법이다. 그렇기에 확률적인 해석이 뒷받침되기 보다는 Algorithm을 통해서 이를 설명한다. 대표적인 방법이 K-Means Clustering이다.
Parametric Approach
확률적 분포를 가정한 후, Parameter를 찾아가는 방식으로, 대표적인 방법이 Gaussian 분포를 가정하고 찾아나가는 Gaussian Mixture Model(GMM, or MoG, Mixture of Gaussian)이 있다.

따라서, Clustering을 대표하는 K-means Clustering과 GMM을 각 각 살펴보도록 하겠다.

K-Means Clustering

K-Means Clustering은 K개의 평균값을 통한 Clustering으로 해석하면 의미 파악이 쉽다. 즉, K개의 Partition을 만들기 위해서 K개의 평균값을 찾아 이를 기반으로 더 가까운 평균값에 속하는 Partition에 data를 분배하는 방식이다.

그렇다면, 우리가 구해야할 값은 각 data가 어느 Partition에 속하는지에 대한 정보( $\bold{r}\leftarrow\text{one hot vector}$ )와 각 Partition의 평균값( $\mu$ )이다. 즉, K-means Clustering에서는 기존 data들을 통해서 K개의 평균값(K-means)을 찾아서(Learning) 이후에 추가로 들어올 data에 대해서도 똑값은 K-means를 통해서 Partition을 찾을 수 있다(Inference).또는 모든 data를 저장해두었다가 K-means를 다시 계산하는 방법도 있다(Online K-means).

그렇다면, $\boldsymbol{\mu}(=\{\mu_{1}, \mu_{2}, \cdots, \mu_{K}\})$ 와 $\bold{R}$ (모든 data의 $\bold{r}$ 로 이루어진 Matrix)을 어떻게 구할 수 있을까? 이에 대한 해답은 다음과 같은 Cost Function을 제시하는 것으로 해결할 수 있다.

\mathcal{L} = \min_{\boldsymbol{\mu}}\min_{\bold{R}} \sum_{i \in \{1,2, \cdots, N\}}\sum_{k \in \{1, 2, \cdots, K\}}\bold{R}_{ik}||x_{i} - \mu_{k}||^{2}

현재 data의 point로 부터 가장 가까운 평균을 선택하는 경우를 최대화해야 해당 값이 가장 작아질 수 있다는 것을 알 수 있다. 즉, 여기서는 평균과의 거리를 유사성의 지표로 사용한 것이다. 여기서는 Euclidean distance(L2-norm)를 사용했지만, Manhatan distance(L1-norm)을 활용할 수도 있고 아예 다른 지표를 활용할 수도 있다. 중요한 것은 Cost Function이 아래와 같은 form을 가진다는 것이다.

\mathcal{L} = \min_{\boldsymbol{\mu}}\min_{\bold{R}} \sum_{i \in \{1,2, \cdots, N\}}\sum_{k \in \{1, 2, \cdots, K\}}\bold{R}_{ik}\times(\text{Similarity measure})

그렇다면, 실제로 위에서 제시한 Cost Function을 활용하여 어떻게 $\boldsymbol{\mu}$ 와 $\bold{R}$ 을 구할 수 있을까? minimize하고자하는 요소가 두 개이기 때문에 미분을 하기도 다소 난해하다. 따라서, 여기서는 EM Algorithm이라는 방식을 제시한다. 이에 대해서는 다음 Posting에 대해서 자세히 다루겠지만, 간단히 설명하자면 하나의 Variable을 Random하게 지정하고, 다른 Variable의 최적값을 구한 후 이를 다시 대입하고 반대 Variable을 최적값으로 구하기를 반복하면서 더 이상 Variable이 유의미하게 변경되지 않을 때까지 반복해서 구한 값이 최적값과 근사한다는 점을 활용한 Algorithm이다. 지금은 다소 엉뚱할 수 있지만, 지금은 해당 방법을 사용하도록 하겠다. 증명이 궁금하다면, 해당 Posting(🔗 [ML] 10. EM Algorithm)을 참고하자.

따라서, 우리가 수행할 과정은 다음과 같다.

$\boldsymbol{\mu}$ 를 랜덤하게 초기화한다.
Assignment step: $\boldsymbol{\mu}$ 가 주어졌을 때, $\bold{R}$ 을 구한다. $R_{ik} = \begin{cases} 1 & \text{if}\quad k = \argmin_{k}||x_{i} - \mu_{k}||^{2} \\ 0 & \text{otherwise} \end{cases}$
Update step: $\bold{R}$ 이 주어졌을 때, $\boldsymbol{\mu}$ 를 구한다.
우리가 분류한 $R$ 을 활용하여 각 k에 속하는 data의 평균을 통해서 $\boldsymbol{\mu}$ 를 구한다. $\mu_{k} = \frac{\sum_{i=1}^{N}R_{ik}x_{i}}{\sum_{i=1}^{N}R_{ik}}$
특정값으로 $\boldsymbol{\mu}$ 가 수렴할 때까지 2번, 3번 과정을 반복한다.

아래는 이 과정을 그림을 통해서 표현한 것이다.

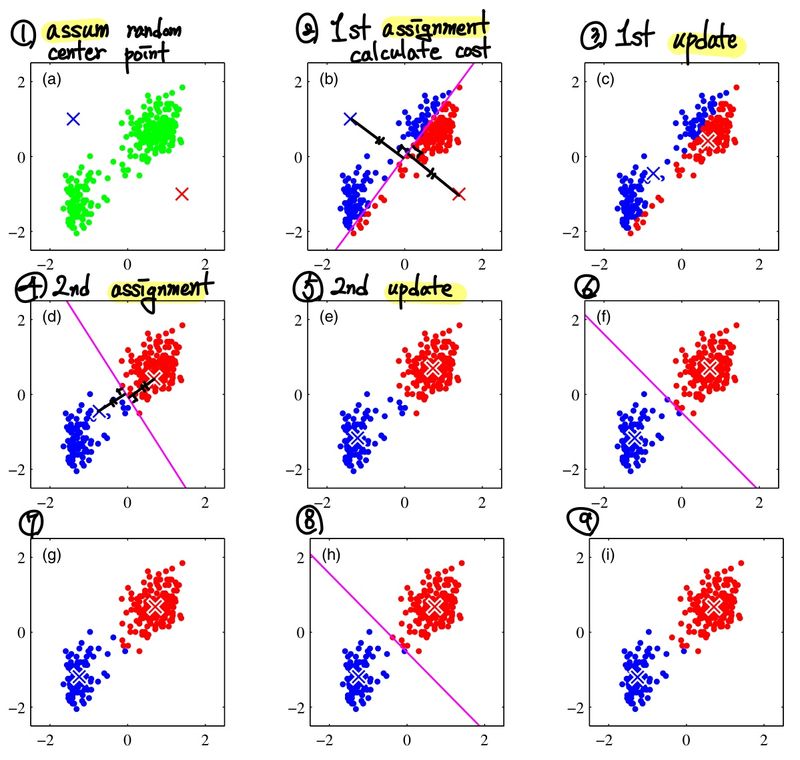
ml-clustering-1

K-means 방식은 위와 같은 Iteration 절차를 많이 수행하지 않아도 몇번의 수행만으로 수렴한다는 것을 관측할 수 있다. 또한, Assignment 시에는 $O(KND)$ 의 시간이 소모되고, Update 시에는 $O(N)$ 만큼의 시간이 소모되기 때문에 무겁지 않고, 굉장히 간단하다는 장점을 갖고 있다. 하지만, 이 방법은 Global Optimal을 찾을 것이라는 확신을 줄 수 없다. 그렇기에 초기값을 어떻게 잡느냐에 따라서 결과가 크게 변할 수도 있다. 뿐만 아니라, outlier data에 대해서도 굉장히 민감하게 반응한다는 단점이 있다. 예를 들어, 아래 사진에서 왼쪽보다 오른쪽이 더 성공적인 Clustering이라고 말할 수 있을 것이다.

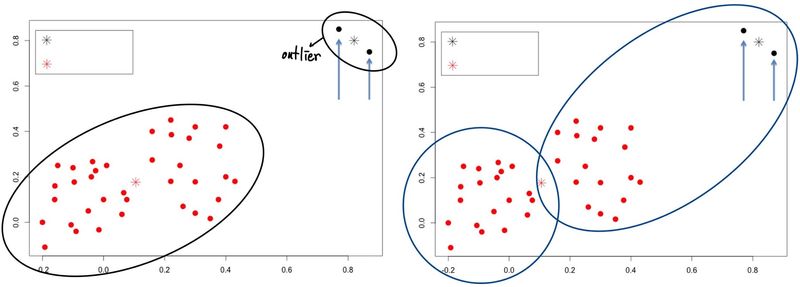
ml-clustering-2

이를 해결하기 위한 방법으로 다음과 같은 방법들이 제시되었다.

K-means++: 초기값을 잘 설정하기 위한 방법으로, 초기값을 잘 설정하면 수렴하는 속도가 빨라지고, Global Optimal에 수렴할 가능성이 높아진다.
K-mendoids: K-means에서는 중심점을 data의 평균으로 설정했지만, K-mendoids에서는 중심점을 data의 중간값으로 설정한다. 이렇게 하면 outlier에 민감하지 않게 된다.

Soft K-means

마지막으로 K-means Clustering에서 확률적인 접근을 시도한 방법 또한 소개하겠다. 앞 서 본 (Hard)K-means에서는 $\bold{R}_{ik}$ 를 0 또는 1로 보았다. 하지만, 이를 확률적으로 표현하는 것에 대해서 생각해 볼 수 있다. 즉, 다음과 같이 soft-max function을 활용한다면 표현이 가능할 것이다.

\bold{R}_{ik} = \frac{\exp(-\beta||x_{i}-\mu_{k}||^{2})}{\sum_{l \in {1, 2, \cdots, K}} \exp(-\beta||x_{i}-\mu_{l}||^{2})}

이렇게 확률적으로 표현하게 되면, 우리는 추가적인 정보를 활용할 수 있다. 대표적으로 특정 Cluster로 해당 확률이 편향되어 있을 수록 더 좋은 분류일 것이라는 사전 지식(Prior)을 활용할 수 있다. 따라서, 우리는 다음과 같이 Cost Function을 변경할 수 있다.

\mathcal{L} = \min_{\boldsymbol{\mu}}\min_{\bold{R}} \sum_{i \in \{1,2, \cdots, N\}}\sum_{k \in \{1, 2, \cdots, K\}}\bold{R}_{ik}||x_{i} - \mu_{k}||^{2} - \frac{1}{\beta}\sum_{i \in \{1,2, \cdots, N\}}\sum_{k \in \{1, 2, \cdots, K\}}\bold{R}_{ik}\log\bold{R}_{ik}

뒷 부분에 새로 추가된 $-\frac{1}{\beta}\sum_{i \in \{1,2, \cdots, N\}}\sum_{k \in \{1, 2, \cdots, K\}}\bold{R}_{ik}\log\bold{R}_{ik}$ 는 $R_{ik}$ 가 확률이 되었기 때문에 사실상 Entropy를 의미한다. Entropy는 균형잡힌 분포일 수록 커지고, skew된 경우에는 작아지기 때문에 적절한 지표라고 할 수 있다. $\beta$ 는 이러한 prior를 얼마나 사용할지에 대한 hyperparameter이다. $\beta$ 가 클 수록 사실상 Hard K-means와 동일한 결과를 얻게 되고, $\beta$ 가 작을 수록 Entropy를 더 중요시하는 결과를 얻게 된다.

Gaussian Mixture Model

Gaussian Mixture Model, 일명 GMM은 Finite Mixture Model의 일종이다. Finite Mixture Model은 우리가 추정하고자 하는 확률 분포가 다양한 확률 분포 몇 개의 조합으로 이루어진 분포라고 가정하고, 해당 확률 분포의 Parameter를 학습(Learning) 단계에서 찾아내고, 이를 이용해서 새로운 data에 대해서 추정(Inference)하는 방식이다.

p(x) = \sum_{k \in \{1, 2, \cdots, K\}}p(x, z=k) = \sum_{k \in \{1, 2, \cdots, K\}}p(x|z=k)p(z=k) = \sum_{k \in \{1, 2, \cdots, K\}}p_{k}(x)p(z=k)

여기서 $z$ 는 관측할 수 없는 latent(hidden) variable로 data가 몇 번째 확률 분포에 속할 것인지를 의미한다. 따라서, $p(z=k)$ k번째 분포에 속할 확률이라고 볼 수 있다. 대게 이것이 어느정도로 확률 분포를 섞는지를 의미하기 때문에 mixing parameter라고도 부른다.

이에 따라 GMM은 각 $p_{k}(x)$ 가 Gaussian Distribution이라고 가정하는 Finite Mixture Model인 것이다.

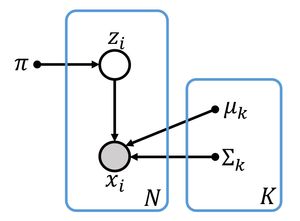
ml-gmm-graphical-form

그렇다면, 우리는 다음과 같이 Graphical Model 형태로 Finite Mixture Model을 생성할 수 있다. 여기서 $\pi,\, \mu,\, \Sigma$ 는 Parameter를 의미한다.

$\pi_{k} = p(z = k)$
$\mu_{k} = E[x|z=k]$ 즉, Gaussian의 기댓값을 의미한다.
$\Sigma_{k} = Cov[x|z=k]$ 즉, Gaussian의 분산을 의미한다.

이를 통해서 우리는 위에서 제시한 확률을 다음과 같이 재정의할 수 있다. (Joint Probability를 Bayesian Network로 푼 식이다. 모르겠다면, 🔗 [ML] 8. Graphical Model에서 Bayesian Network를 다시 살펴보고 오자.)

\begin{align*} p(x) &= \sum_{k \in \{1, 2, \cdots, K\}}p(x, z=k) \\ &= \sum_{k \in \{1, 2, \cdots, K\}}p(z=k| \pi_{k})p(x|z=k, \mu_{k}, \Sigma_{k}) \\ &= \sum_{k \in \{1, 2, \cdots, K\}}\pi_{k}\mathcal{N}(x|\mu_{k}, \Sigma_{k}) \end{align*}

여기서 우리가 실제로 추측(Inference)을 할 때에는 $p(z|x)$ 가 필요하다. 이는 우리가 posterior를 활용해서 구할 수 있다.

\begin{align*} \hat{k} &=\argmax_{k}p(z=k|x) \\ &= \argmax_{k}\frac{p(x|z=k)p(z=k)}{p(x)} \\ &= \argmax_{k}p(x|z=k)p(z=k)\\ &= \argmax_{k}\pi_{k}\mathcal{N}(x|\mu_{k}, \Sigma_{k}) \end{align*}

학습(Learning)을 할 때에는 결국 $\pi,\, \mu,\, \Sigma$ 이 세 개의 parameter 값을 찾는 것이 중요하다. 이것은 우리가 Parametric Estimation에서 줄기차게 했던 MLE를 이용하면 된다. 이를 위한 Likelihood는 다음과 같다.

\begin{align*} \mathcal{L}(\pi,\, \mu,\, \Sigma) &= \log{p(\mathcal{D} | \pi,\, \mu,\, \Sigma)} \\ &= \log{\prod_{i=1}^{N}{p(x_{i} | \pi,\, \mu,\, \Sigma)}} \\ &= \sum_{i=1}^{N}{\log{p(x_{i}| \pi,\, \mu,\, \Sigma)}} \\ &= \sum_{i=1}^{N}{\log{\sum_{k=1}^{K}{\pi_{k}\mathcal{N}(x_{i}|\mu_{k}, \Sigma_{k})}}} \end{align*}

하지만, 이것을 단순한 Optimization Technique으로는 풀 수 없다. 왜냐하면, 단순한 미분으로 각 parameter를 구할 수 없기 때문이다. 따라서, EM Algorithm을 이용해서 풀어야 한다. (이것은 🔗 [ML] 10. EM Algorithm에서 다룬다.)

따라서, 아래 그림과 같이 임의의 $\pi,\, \mu,\, \Sigma$ 를 가정한 상태에서 data에 알맞는 최적의 Cluster set을 구하고, data에 cluster가 label된 상태에서 최적의 $\pi,\, \mu,\, \Sigma$ 를 구하는 과정을 반복하는 것이다.

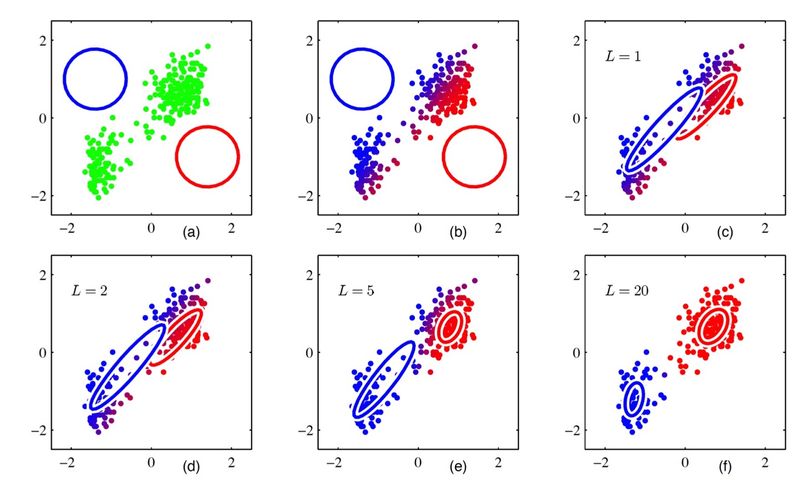
ml-gmm-1

그렇다면, 이를 실제로 어떻게 하는지를 알아보도록 하겠다. 하지만, 그냥 모든 Gaussian 형태를 위한 방법을 사용하면 다소 식이 복잡해지기 때문에 isotropic Gaussian(모든 방향에서 분산이 동일한 Gaussian)을 가정으로 하겠다.

또한, 다음과 같은 요소를 추가로 정의하자.

$z_{i} \in \{1, 2, \cdots, K\}$ : $i$ 번째 data가 속하는 cluster의 index
$z_{ik} = \begin{cases} 1 & \text{if } z_{i} = k \\ 0 & \text{otherwise} \end{cases}$
$\theta_{k} = (\pi_{k},\, \mu_{k},\, \Sigma_{k})$ : $k$ 번째 cluster를 위한 parameter의 집합
$\theta = (\pi,\, \mu,\, \Sigma)$ : parameter의 집합

앞 서 말한 바와 같이 이제 우리는 $\theta$ 를 구하는 과정에서 $z_{i}$ 에 해당하는 정보도 알고 있다. 따라서, Likelihood 식도 변형되어야 한다.

\begin{align*} \mathcal{L}(\theta) &= \log{p(\mathcal{D} | \theta)} \\ &\geq \log{p(X, Z | \theta)} \\ &= \sum_{i=1}^{N}{\log{p(x_{i}, z_{i}| \theta)}} \\ &= \sum_{i=1}^{N}{\log{p(z_{i} | \theta) \times p(x_{i}| z_{i}, \theta)}} \\ &= \sum_{i=1}^{N}{\log{(\prod_{k=1}^{K}{\pi_{k}^{z_{ik}}} \times \prod_{k=1}^{K}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)^{z_{ik}}})}} \\ &= \sum_{i=1}^{N}{\sum_{k=1}^{K}\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})^{z_{ik}}}} \\ &= \sum_{i=1}^{N}{\sum_{k=1}^{K}z_{ik}\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})}} \\ \end{align*}

이에 따라서 우리는 EM Algorithm의 $\mathcal{Q}$ 를 다음과 같이 구할 수 있다.

\begin{align*} \mathcal{Q}(\theta; \theta^{\prime}) &= \sum_{i=1}^{N}E_{z_{i}|x_{i}, \theta^{\prime}}[\log p(x_{i}, z_{i} | \theta)] \\ &= \sum_{i=1}^{N}E_{z_{i}|x_{i}, \theta^{\prime}}[\sum_{k=1}^{K}z_{ik}\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})}] (\because \text{위의 식에서 3번째 줄을 참고})\\ &= \sum_{i=1}^{N}\sum_{k=1}^{K}E_{z_{i}|x_{i}, \theta^{\prime}}[z_{ik}\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})}] \\ &= \sum_{i=1}^{N}\sum_{k=1}^{K}E_{z_{i}|x_{i}, \theta^{\prime}}[z_{ik}\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})}] \\ &= \sum_{i=1}^{N}\sum_{k=1}^{K}E_{z_{i}|x_{i}, \theta^{\prime}}[z_{ik}]\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})} \\ \end{align*}

따라서, 우리는 각 step을 다음과 같이 정의할 수 있다.

E-step
$\mathcal{Q}$ 에서 parameter( $\pi,\, \mu,\, \Sigma$ )를 제외하고, 아직 미지수로 남아있는 값은 $E_{z_{i}|x_{i}, \theta^{\prime}}[z_{ik}]$ 이다. 즉, 이 값만 구하면 $\mathcal{Q}$ 를 구했다고 할 수 있다.
$\begin{align*} E_{z_{i}|x_{i}, \theta^{\prime}}[z_{ik}] &= \sum_{k=1}^{K}{z_{ik}p(z_{i} = k | x_{i}, \theta^{\prime})} \\ &= p(z_{i} = k^{*} | x_{i}, \theta^{\prime}) = r_{ik^{*}} \end{align*}$
결국 우리가 해당 단계에서 구할 것은 관측 가능한 data와 이전 parameter가 주어졌을 때, 속하게 되는 cluster에서의 확률을 구하는 것이다. 이것을 모든 data에 대해서 구하면, $\mathcal{Q}$ 에서 parameter를 제외한 모든 부분을 구할 수 있다. 따라서, 식을 좀 더 정리하면 다음과 같은 결론을 얻을 수 있다.
$\begin{align*} E_{z_{i}|x_{i}, \theta^{\prime}}[z_{ik}] = r_{ik^{*}} &= \frac{p(x_{i}, z_{i}=k^{*} | \theta^{\prime})}{p(x_{i}|\theta^{\prime})} \\ &= \frac{\pi_{k^{*}}^{\prime}{\mathcal{N}(x_{i}|\mu_{k^{*}}^{\prime}, \Sigma_{k^{*}}^{\prime} I)}}{\sum_{l=1}^{K}{\pi_{l}{\mathcal{N}(x_{i}|z_{i} = l, \mu_{l}, \Sigma_{l} I)}}} \end{align*}$
M-step
결론적으로 우리는 다음과 같은 $\mathcal{Q}$ 와 constraint를 얻었다.
$\begin{align*} \text{maximize}&\quad \mathcal{Q}(\theta; \theta^{\prime}) = \sum_{i=1}^{N}\sum_{k=1}^{K}r_{ik}\log{({\pi_{k}}{\mathcal{N}(x_{i}|\mu_{k}, \Sigma I)})} \\ \text{subject to}&\quad \sum_{k=1}^{K}{\pi_{k}} = 1 \end{align*}$
이제 우리는 이를 Optimization 방식을 활용하여 풀기만 하면 끝이다. (🔗 참고(Base Knowledge))
$\begin{align*} \mu_{k} &= \frac{\sum_{i=1}^{N}{r_{ik}x_{i}}}{\sum_{i=1}^{N}{r_{ik}}} \\ \Sigma_{k} &= \frac{\sum_{i=1}^{N}{r_{ik}||x_{i} - \mu_{k}||^{2}}}{\sum_{i=1}^{N}{r_{ik}}} \\ \pi_{k} &= \frac{1}{N}\sum_{i=1}^{N}{r_{ik}} \end{align*}$

마지막으로 짚고 넘어갈 것은, 바로 K-means Clustering은 사실 GMM의 하나의 special case라는 것이다. 만약, 우리가 $\pi_{k},\, \Sigma_{k}$ 를 모두 같은 값으로 설정하면, $\pi_{k} = \frac{1}{K}$ 이고 $\Sigma_{k} = \Sigma$ 가 된다고 하자. 이때 EM algorithm을 살펴보면 다음과 같다.

E-step $r_{ik} = \begin{cases} 1 & k = \argmax_{l\in \{1, 2, \cdots, K\}} p(x_{i}|z_{i} = l, \mu_{l}, \Sigma) \\ 0 & \text{otherwise} \end{cases}$ 이는 사실상 K-means Clustering에서 중심과의 거리를 통해서 구했던 것과 매우 유사한 식이다.
M-step $\begin{align*} \mu_{k} &= \frac{\sum_{i=1}^{N}{r_{ik}x_{i}}}{\sum_{i=1}^{N}{r_{ik}}} \\ \pi_{k} &= \frac{1}{N}\sum_{i=1}^{N}{r_{ik}} \end{align*}$ $\pi_{k}$ 가 추가되기는 했지만, $\mu_{k}$ 를 구하는 식은 완전 동일하다.

Reference

Tumbnail : Photo by Markus Winkler on Unsplash