[ML] 6. Neural Network

Intro

우리는 Linear Regression, Logistic Regression, SVM을 거치며 data로 부터 유의미한 pattern을 발견하는 과정을 알아보았다. 이 과정은 우리에게 명확한 식 하나를 제시하였고, 모든 과정을 우리가 제어할 수 있게 하였다. 하지만, 실제 데이터를 우리가 모두 명확하게 이해할 수 있는 형태로 분류할 수 있는 것인지는 의문이 들 수 있다. 그렇다면, 우리가 이해하지는 못하지만, 알아서 최적의 결과를 가져오게 할 수 있는 방법이 있을까? 이런 마법같은 일에 대한 아이디어를 제시하는 것이 Neural Network이다. 대게 알지 못하지만 input이 들어왔을 때, 이를 처리해서 output을 전달하는 시스템을 우리의 신체에서 찾게 된다. 바로 우리 몸을 이루는 신경망이다. 예시로 우리는 눈을 통해 빛이라는 input을 받으면, 우리 눈과 뇌에서 무슨 일이 발생하는지는 모르지만 결과적으로 우리는 물체를 볼 수 있다. 이 과정을 추측의 과정에 도입하면 어떻게 될까?

Perceptron

Perception(인지 능력) + Neuron(신경 세포)의 합성어이다. 중고등학교 생명 수업을 들었다면, 우리의 모든 신경은 뉴런이라는 단위 세포로 이루어진다는 것을 배웠을 것이다. 즉, 우리의 신경 세포를 컴퓨터 공학에서 활용하기 위해서, 수학적으로 변환한 것이다. 형태를 먼저 살펴보자.

y = sign(\bold{w}^{\top}\bold{x} + b)

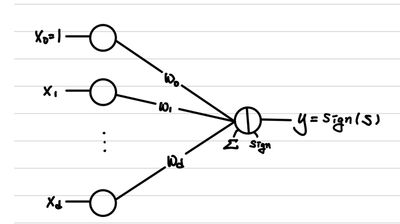
nn-perceptron-1

대단한 것을 기대했다면 실망하겠지만, simple한 것이 최고라는 연구의 진리에 따라서 위의 식은 꽤나 합리적이다. 우리가 Linear Regression과 Logistic Regression을 배웠으니 알 것이다. 이는 사실 Linear Regression을 이용해서 우리가 Classification을 수행할 때 사용했던 식이다. 즉, perceptron 하나는 input을 선형으로 구분할 수 있도록 하는 decision boundary를 찾는 것과 같다.

Optimization

그렇다면, 해당 perceptron을 통해서 모든 데이터를 구분하기 위해서는 다음을 만족하는 $\bold{w}$ 를 찾아야 한다.

y_{n} = \begin{cases} 1 &\text{ if } \bold{x}_{n} \in \mathcal{C}_{1} \\ -1 &\text{ if } \bold{x}_{n} \in \mathcal{C}_{2} \\ \end{cases}

y_{n}\bold{w}^{\top}\bold{x}_{n} \gt 0, \forall n

결국 Loss 함수는 perceptron의 잘못된 classification 결과를 최소화하는 것이다.

\mathcal{J}(\bold{w}) = - \sum_{n \in \mathcal{M}(\bold{w})}{y_{n}\bold{w}^{\top}\bold{x}_{n}} \quad( \mathcal{M}(\bold{w}) = \{ n : y_{n}\bold{w}^{\top}\bold{x}_{n} \} )

\nabla_{\bold{w}}\mathcal{J}(\bold{w}) = - \sum_{n \in \mathcal{M}(\bold{w})}{y_{n}\bold{x}_{n}}

따라서, 우리가 사용할 수 있는 Gradient Descent식은 다음과 같다.

\bold{w}_{t+1} = \bold{w}_{t} + \alpha\sum_{n \in \mathcal{M}(\bold{w})}{y_{n}\bold{x}_{n}}

간단한 예시로 AND, OR Gate를 percentron을 통해 표현해보자.

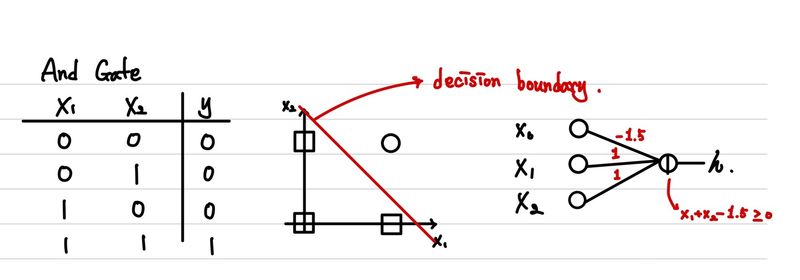
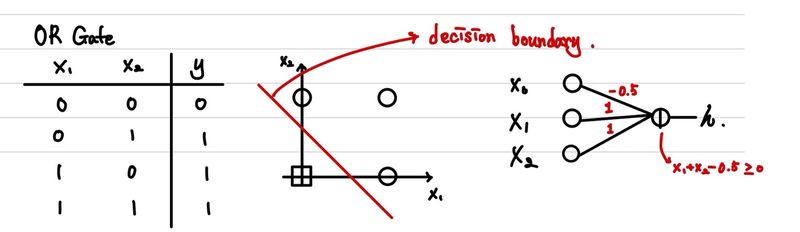
nn-and-gate nn-or-gate

하지만, 우리가 다루는 데이터는 항상 완벽하게 선으로 나뉘어지지는 않는다. 하나의 perceptron으로는 아래의 XOR조차도 구분해낼 수 없다.

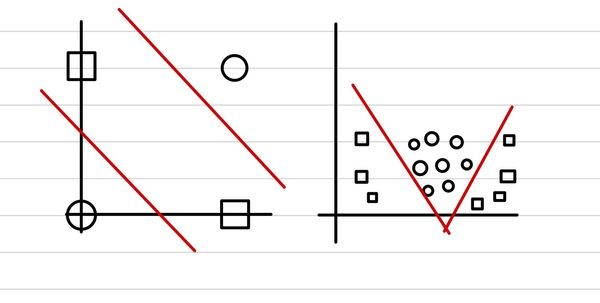
nn-multi-line-example

Multilayer Perceptron

위의 문제를 해결하기 위해서 나온 것이 perceptron을 다층으로 쌓아서 해결하는 방법이다. 이제는 하나의 신경세포였던 perceptron을 진짜 신경망처럼 연결해보자는 것이다.

먼저 추상적인 예시를 생각해보자. 우리가 XOR Gate를 만들기 위해서는 어떤 Gate를 결합해야할까?

a \oplus b = ab + \bar{a}\bar{b}

우리는 AND Gate 2개 연산을 수행하고, 해당 결과값을 이용해서 OR Gate 연산을 수행하면 XOR Gate를 표현할 수 있다는 것을 알고 있다. 그렇다면, 각 Gate는 우리가 perceptron으로 나타낼 수 있었는데 그냥 이것을 gate로 표현하듯이 똑같이 나타내면 풀 수 있지 않을까?

그래서 직접 수행해보면 다음과 같은 값을 구할 수 있다.

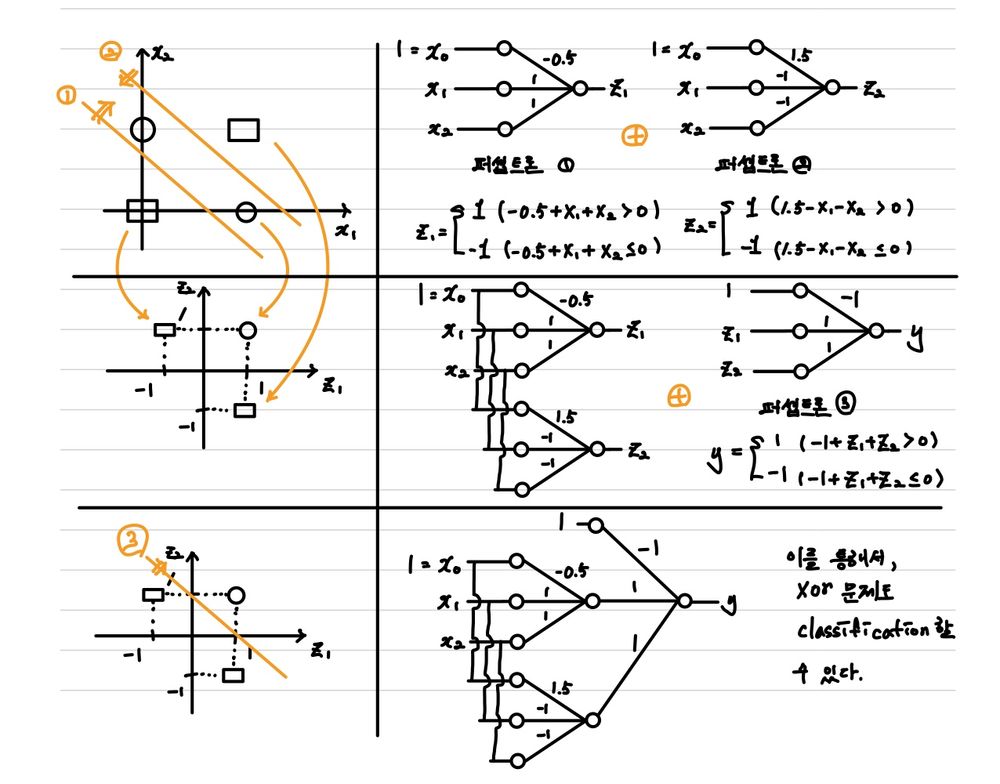
nn-xor-gate


1 🤔 Insight
2
3 위의 과정을 보다보면 놀라운 것을 하나 발견할 수 있다. 바로 왼 쪽 그림의 변화이다. 
4 첫번째, 두 개의 perceptron을 통해서 만들어진 output이 이루는 결과값의 형태로 feature를 변환하면, 
5 하나의 perceptron으로 decision boundary를 그릴 수 있다는 것이다. 
6 이는 마치 이전 linear regression에서 배웠던 basis function(ϕ)이 했던 역할이다.
7
8 그렇다면, 이를 더욱 확장해보자. 
9 만약 해당 Layer가 더 깊어진다고 해도, 출력 직전의 layer는 단순히 이전 모든 layer는 입력 데이터를 가공해서
10feature를 변환하는 하나의 basis function(ϕ)를 취한 것으로 이해할 수 있다.

결론적으로 우리는 더 복잡하고, 어려운 문제의 경우에도 더 깊게 신경망을 구성하면 결국은 문제를 풀 수 있다는 것이다.

Universal Approximation Theorem

위와 같은 깊은 신경망 구조를 이용하자는 주장도 있지만, 이와 유사하게 넓은 신경망을 쓰자는 주장도 존재했다.

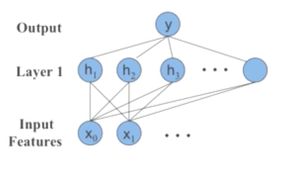
nn-universal-approx-theorem-1

만약, 우리가 하나의 Layer와 output에서 최종 output perceptron만 갖고 처리를 한다면, 결국 여러 perceptron의 weighted 합으로 볼 수 있다. 그 경우 우리는 계단 함수의 weighted 합으로 생각할 수 있는데 perceptron이 많아질 수록 촘촘해지며 정답과 유사한 추론이 가능해진다.(마치 적분의 개념과 유사하다. 물론 이는 추상적인 설명이기 때문에 실제로는 계단함수의 합이기 때문에 좀 다르다.)

nn-universal-approx-theorem-2

위의 그림을 보면 이해할 수 있다. 하지만, 이 방식은 결국 모든 함수 형태를 기억하는 것이다.(memorizer) 이것은 input data가 많아질 수록 복잡도가 급격하게 증가하기 때문에 학습과 예측과정에 굉장히 많은 시간을 소모한다.

Multilayer Optimization(Backpropagation)

그렇다면, 넓은 신경망이 한계가 있으니 선택지는 input과 output 사이의 layer(hidden layer)의 갯수를 늘려서 깊은 신경망을 만드는 것이다. 하지만, 우리가 사용하고 있는 perceptron은 sign함수로 감싸져있기 때문에 미분 시에 기울기가 0이라는 문제를 갖는다. 또한, 그렇다고 정답의 갯수를 이용하기에는 각 perceptron의 영향을 전달하기에 부족하다는 것이 명확하다. 따라서, 우리는 perceptron에 있는 정답을 판별하는 함수 sign을 다른 함수로 대체하기로 한다.

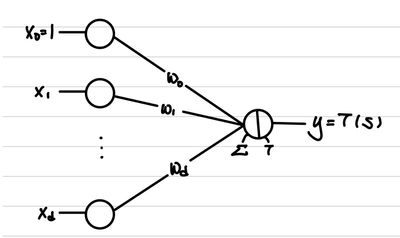
nn-perceptron-2

여기서 이 함수를 우리는 activation function이라고 부르고 대표적으로는 같은 종류가 있다.

sigmoid
우리가 가장 쉽게 생각할 수 있는 함수이다. logistic regression에서 사용해본만큼 기울기값을 효과적으로 가질 수 있다.
tanh
sigmod와 굉장히 유사한 함수이다. 따라서, 비슷한 용도로 사용될 수 있다.
ReLU
출력 시점에서는 사용하지 않지만, 각 각의 hidden layer에서 이를 사용하는 경우가 많다. 왜냐하면, sigmoid 함수는 출력값의 형태가 [0, 1], tanh는 [-1, 1]이기 때문에 반복해서 적용하면, gradient가 사라지는 현상이 발생할 수 있다. 따라서, 기울기를 있는 그대로 적용할 수 있는 이러한 형태를 출력 이전에는 많이 사용한다.
Leaky ReLU
ReLU가 음수값을 완전히 무시하는데 Leaky ReLU는 이러한 데이터가 조금이라도 의미 있는 경우에 사용할 수 있다.
ELU
Leaky ReLU와 비슷한 이유이다.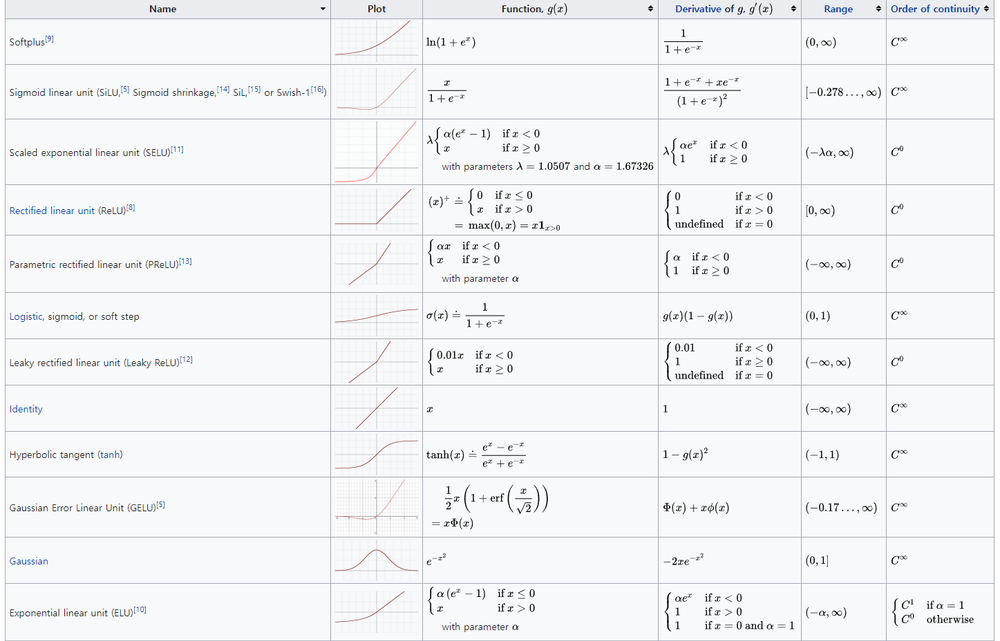

자료가 보이지 않는다면 🔗 wikipedia를 참고하자.

자 이제 실제로 어떻게 optimization을 수행할지를 알아보도록 하자.

먼저, Loss는 가장 마지막 layer(output layer)의 output과 실제 값과의 차이가 될 것이다. 따라서, 다음과 같이 정의할 수 있다.

(아래서 $\bold{h}_{L}$ 은 L번째 layer의 output을 의미한다.)

\begin{align*} \mathcal{L} &= \sum_{n=1}^{N}{\ell(y_n, \bold{h}_L)} \\ &= \sum_{n=1}^{N}{(y_{n} - \bold{h}_{L})^2} \\ &= \sum_{n=1}^{N}{(y_{n} - \sigma(\bold{w}_{L}^{\top}\bold{h}_{L-1} + b_{L-1}))^2} \\ &= \sum_{n=1}^{N}{(y_{n} - \sigma(\bold{w}_{L}^{\top}\sigma(\bold{w}_{L-1}^{\top}\bold{h}_{L-2} + b_{L-2}) + b_{L-1}))^2} \\ &= ... \end{align*}

여기서 중요한 것은 우리는 전체 $\bold{W}$ 를 학습시켜야 한다는 것이다. 우리는 출력층만 학습하는 게 아니라 전체 모든 layer의 $\bold{w}_{i}$ 를 업데이트해야 한다는 것이다.

그러기 위해서는 우리는 ${{\partial\mathcal{L}}\over{\partial \bold{w}_{i}}}$ 를 모두 구해야 한다는 것이다. 아마 가장 습관적으로 하는 행위는 숫자가 작은 값부터 편미분하면서 진행하는 것이다. 하지만, 그렇게 하지말고 반대 순서로 미분을 하라는 것이 backpropagation의 main idea이다.

{{\partial\mathcal{L}}\over{\partial \bold{w}_{L}}} = \sum_{n=1}^{N}\{({\partial \bold{h}_L \over \partial \bold{w}_{L}} )\times\red{-2(y_{n} - \sigma(\bold{w}_{L}^{\top}\bold{h}_{L-1} + b_{L-1}))}\}

{{\partial\mathcal{L}}\over{\partial \bold{w}_{L-1}}} = \sum_{n=1}^{N}\{({\partial \bold{h}_{L} \over \partial \bold{w}_{L-1} })\times\red{-2(y_{n} - \sigma(\bold{w}_{L}^{\top}\bold{h}_{L-1} + b_{L-1}))}\}

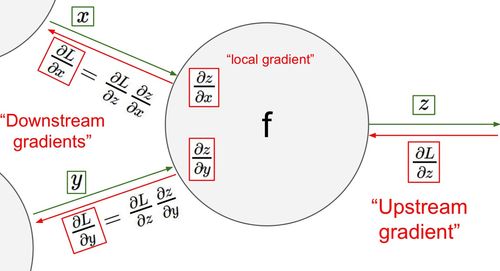
즉, 다음과 같은 chain rule을 이용하는 것이다.

\begin{align*} {{\partial\mathcal{L}}\over{\partial \bold{w}_{L}}} &= \red{ {{\partial\mathcal{L}}\over{\partial \bold{h}_{L}}} } {{\partial\bold{h}_{L}}\over{\partial \bold{w}_{L}}} \\ {{\partial\mathcal{L}}\over{\partial \bold{w}_{L-1}}} &= \red{ {{\partial\mathcal{L}}\over{\partial \bold{h}_{L}}} } {{\partial\bold{h}_{L}}\over{\partial \bold{w}_{L-1}}} \\ &= \red{ {{\partial\mathcal{L}}\over{\partial \bold{h}_{L}}} } {{\partial\bold{h}_{L}}\over{\partial \bold{h}_{L-1}}} {{\partial\bold{h}_{L-1}}\over{\partial \bold{w}_{L-1}}} \\ &= \blue{ {{\partial\mathcal{L}}\over{\partial \bold{h}_{L-1}}} } {{\partial\bold{h}_{L-1}}\over{\partial \bold{w}_{L-1}}} \\ {{\partial\mathcal{L}}\over{\partial \bold{w}_{L-2}}} &= \blue{ {{\partial\mathcal{L}}\over{\partial \bold{h}_{L-1}}} } {{\partial\bold{h}_{L}}\over{\partial \bold{w}_{L-2}}} \\ \end{align*}

우리는 빨간색과 파란색 부분의 연산을 재활용할 수 있다는 것이다. 또한, ${{\partial\bold{h}_{l}}\over{\partial \bold{w}_{l}}}$ 은 굉장히 쉬운 연산이기에 우리가 신경 써서 계산해야 할 값은 매단계를 연결해줄 ${{\partial\bold{h}_{l}}\over{\partial \bold{h}_{l-1}}}$ 이다.

ml-backpropagation

Loss Function

우선 KL-Divergence, Entropy, Cross Entropy에 대한 약간의 이해가 필요하니 이전 Posting(🔗 Base Knowledge)을 살펴보고 오자.

위에서는 자연스럽게 Loss를 계산할 때, Squared Error를 사용하였다. 하지만 경우에 따라서는 다양한 함수를 사용할 수 있다. multiclass classification에서는 Cross Entropy Loss를 사용한다.

우선 Cross Entropy Loss는 대게 L2 Loss(Squared Error)와 같이 비교되어진다. 우선 우리가 이전 🔗 Parametric Estimation에서 MLE를 다룰 때, KL-Divergence를 통해서 MLE가 최적 parameter를 찾을 것이라는 걸 증명한 적이 있다. 그렇다면, 우리가 🔗 Logistic Regression에서 Squared Error를 통해서 Loss를 구했던 공식을 확인해보자.(Gradient Asecent Part)

여기서 우리는 다음과 공식을 봤었다.

\argmax_{\bold{w}} \sum_{n=1}^{N}y_{n}\log{\sigma(\bold{w}^{\top}\bold{x}_{n}) + (1-y_{n})\log{(1-\sigma(\bold{w}^{\top}\bold{x}_{n}))} }

이 공식을 Cross Entropy를 통해서 설명할 수 있다.

\begin{align*} H_{q}(p) &= - \sum_{x \in \Omega}q(x)\log_{2}p(x) \\ &= \sum_{n=1}^{N}{[-y_{n}\log\hat{y}_{n} - (1- y_{n})\log(1-\hat{y}_{n})]} \end{align*}

즉, 여기서 우리가 얻을 수 있는 insight는 Cross Entropy는 sigmoid를 취한 binary classification에서 Squared Error와 같고, 이러한 Cross Entropy를 Squared Error가 할 수 없는 Multiclass에는 적용할 수 있을 것이라는 점이다. 왜냐하면, multiclass classification에 사용되는 Softmax Function을 이용해서 Sigmoid function을 유도하기 때문이다. 잠시 까먹었을까봐 Softmax 함수를 다시 적는다.

\hat{y}_{k} = {{\exp(\bold{w}_{k}^{\top}\bold{x})}\over{\sum_{i=1}^{K}{\exp(\bold{w}_{i}^{\top}\bold{x})}}}

따라서, Cross Entropy Loss를 대입하여 다음과 같은 Loss를 얻을 수 있다.

\mathcal{L} = \sum_{n=1}^{N}\sum_{k=1}^{K}[-y_{k,n}\log\hat{y}_{k,n}],\quad y_{k,n} = p(x_{n} \in C_{k}| x_{n})

여기서 $y_{k,n}$ 은 one-hot encoding된 데이터로, 정답인 class만 1이고 나머지는 모두 0으로 되어 있다. 따라서, multiclass classification에서는 위와 같은 Loss를 주로 사용한다.

이 두가지 뿐만 아니라 여러가지 Loss Function이 이미 존재한다. 예전에 잠깐 설명했던 L1 Loss부터 시작해서 NLLLoss, KLDivLoss 등등 존재하며, data의 특성과 output의 형태에 따라서 우리는 스스로 Loss Function을 새로 정의할 수도 있다.

Reference

Tumbnail : Photo by Markus Winkler on Unsplash
activation function, wikipedia, https://en.wikipedia.org/wiki/Activation_function