[ML] 4. SVM

Intro

우리는 Classification을 하기 위해서 Logistic Regression을 수행하였다. 그 결과 결국 Classification도 결국은 선을 긋는 것이라는 결론을 내리게 되었다. 하지만, 여기서 그치지 않고 하나 더 고민해 볼 수 있는 것이 있다. 바로 주어진 데이터에 대해서 완벽하게 구분하는 decision boundary가 여러 개 있을 때, 어떤 것이 가장 좋은 것일까? 이것에 대한 아이디어를 제시하는 것이 SVM이다. 해당 Posting에서는 이에 대해서 살펴보도록 하겠다.

(Hard Margin) SVM

Soft Vector Machine의 약자로, 위에서 제시한 문제를 해결하기 위해서 Margin이라는 것을 도입하였다.

Margin

Margin이란 decison boundary와 가장 가까운 각 class의 두 점 사이의 거리를 2로 나눈 값이다.

svm-1

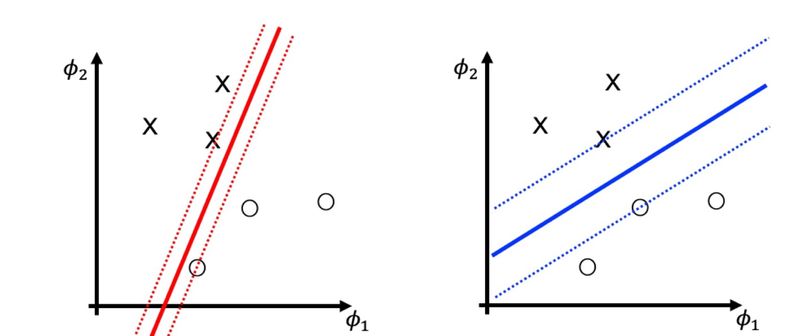
위의 그림은 똑같은 데이터 분포에서 대표적인 decision boundary 두 개를 제시한 것이다. 여기서 우리는 굉장히 많은 decision boundary를 그릴 수 있다. 그 중에서도 파란색 실선이 직관적으로 가장 적절한 decision boundary가 될 것이라고 짐작할 수 있다. 그 이유는 필연적으로 data는 noise에 의한 오차가 발생할 수 있는데 실제 데이터의 오차의 허용 범위를 우리는 margin(=capability of unexpected noise)만큼 확보할 수 있다는 의미로 이를 해석할 수 있다. 따라서, 이 margin을 크게 하면 할 수록 좋은 성능을 가지는 선을 그을 수 있을 것이라는 결론을 내릴 수 있다.

이것이 SVM의 핵심 아이디어이다.

그렇다면, margin을 수학적으로 정의해보자. 우리가 decision boundary를 $f(\bold{x}) := \bold{w}^{\top}\bold{x} + b = 0$ 이라고 한다면, 점( $\bold{x}_{i}$ )과 vector 직선 vector 사이의 거리 공식을 통해서 ${{|f(\bold{x}_{i})|}\over{||\bold{w}||^{2}}}$ 라는 것을 알 수 있다.

따라서 margin은 수학적으로 다음과 같다.

\min_{i}{{|f(\bold{x}_{i})|}\over{||\bold{w}||^{2}}}


1 🤔 Canonical(법칙까지는 아니지만 사실상 표준화된) SVM
2
3 SVM에서는 f(x) = 0인 등식 형태를 같는다. 즉 f(x)에 어떤 값을 곱해도 똑같다는 것이다.
4 그런데 margin의 크기를 구할 때에는, w와 b에 어떤 값이 곱해진다면 이 값이 굉장히 달라지게 된다.
5 따라서, 일반적으로 우리는 margin에서의 |f(x)| = 1이 될 수 있도록 설정한다. 
6 이렇게 하면 계산이 굉장히 쉬워진다.

svm-2

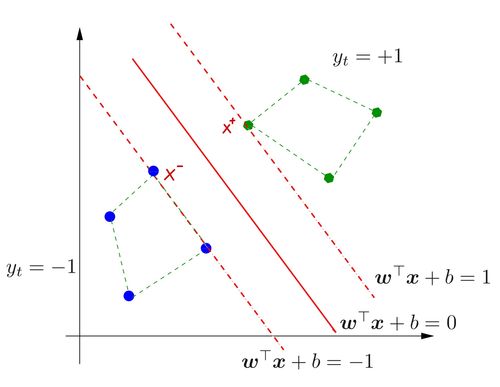
따라서, 우리는 위의 그림과 같은 형태로 $\bold{x}^{-}$ 와 $\bold{x}^{+}$ 를 찾을 수 있는 것이다.

이제 마지막으로 margin을 정의해보자.

\begin{align*} \rho &= {1\over2}\{ {{|f(\bold{x}^{+})|}\over{||\bold{w}||^{2}}} - {{|f(\bold{x}^{-})|}\over{||\bold{w}||^{2}}} \} \\ &= {1\over2}{1\over{||\bold{w}||^{2}}}\{\bold{w}^{\top}\bold{x}^{+} - \bold{w}^{\top}\bold{x}^{-}\} \\ &= {1\over{||\bold{w}||^{2}}} \end{align*}

Optimization

그렇다면, 이제 우리는 문제를 해결할 준비가 된 것이다. 우리가 하고자 하는 것은 margin을 최대화하면서도, 모든 data를 오류없이 분류하는 것이다. 이는 다음과 같은 Constraint Optimization 형태로 변환할 수 있다.

\begin{align*} \text{maximize} \quad & {1\over{||\bold{w}||^{2}}} &\\ \text{subject to} \quad & y_{i}(\bold{w}^{\top}\bold{x}_{i} + b) \geq 1, & i = 1, ..., N \end{align*}

Conditional Optimization은 이전 Posting([ML] 0. Base Knowledge)에서 다룬바 있다. 해당 내용에 대해 미숙하다면 한 번 살펴보고 오도록 하자.

위 내용을 숙지하였다면, 위의 폼이 다소 바뀌어야 한다는 것을 알 것이다. 해당 형태를 바꾸면서, minimize 형태를 미분이 간편할 수 있도록 바꾸도록 하겠다.

\begin{align*} \text{minimize} \quad & {1\over2}||\bold{w}||^{2} &\\ \text{subject to} \quad & 1 - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b) \leq 0, & i = 1, ..., N \end{align*}

우선 lagrangian은 다음과 같다.

\mathcal{L} = {1\over2}||\bold{w}||^{2} + \sum_{i=1}^{N}\alpha_{i}(1 - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b))

이것에 KKT Condition을 적용하여 정리하면 다음과 같은 등식을 얻을 수 있다.

\bold{w} = \sum_{i=1}^{N}\alpha_{i}y_{i}\bold{x}_{i}

\sum_{i=1}^{N}\alpha_{i}y_{i} = 0

이를 $\mathcal{L}$ 에 대입하여 식을 정리하면, 다음과 같다.

\mathcal{L} = -{1\over2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}\bold{x}_{i}^{\top}\bold{x}_{j} + \sum_{i=1}^{N}\alpha_{i}

이제 이것을 이용해서 Dual Problem을 정의하면 다음과 같다.

\begin{align*} \text{maximize} \quad & -{1\over2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}\bold{x}_{i}^{\top}\bold{x}_{j} + \sum_{i=1}^{N}\alpha_{i} &\\ \text{subject to} \quad & \sum_{i=1}^{N}\alpha_{i}y_{i} = 0, & \\ & \alpha_{i} \geq 0, & i = 1, ..., N \end{align*}

이 식에서 눈여겨 볼점은 바로 constraint 부분이다. 이 과정을 통해서 결론적으로 constraint 부분이 부등식에서 등식이 되었다. 이는 연산 과정을 매우 간단하게 한다. 뿐만 아니라 $\bold{x}_{i}^{\top}\bold{x}_{j}$ 는 한 번 계산하면, 전체 과정에서 계속해서 재사용할 수 있기 때문에 컴퓨팅 시에는 굉장한 이점을 발휘할 수 있다. 따라서, 실제로 값을 구할 때에는 이것을 이용하여 값을 구하는 것이 가장 일반적이다.

(Soft Margin) SVM

SVM의 모든 절차를 살펴본 것 같지만, 우리가 간과한 사실이 하나 있다. 바로 그것은 우리는 data가 하나의 선을 통해서 완벽하게 나뉘어진다고 가정했다. 하지만, 실제 데이터는 그렇지 않을 가능성이 크다. 따라서, 우리는 어느 정도의 오차를 허용할 수 있도록 해야 한다. 이를 slack( $\zeta$ )이라고 한다.

svm-2

이를 적용하면, 우리의 목적함수와 제약 조건을 변경해야 한다. 이를 변경하는 방법은 두 가지가 존재하는데 각 각 slack variable의 L2-norm을 목적함수에 더하는 방식과 L1-norm을 더하는 방식이다.

L2-norm Optimization

먼저 L2-norm을 더하는 방식을 알아보자

\begin{align*} \text{minimize} \quad & {1\over2}||\bold{w}||^{2} + C\sum_{i=1}^{N}\zeta_{i}^{2} &\\ \text{subject to} \quad & 1 - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b) - \zeta_{i} \leq 0, & i = 1, ..., N \end{align*}

여기서 $C$ 는 margin 최대화와 slackness 정도의 상대값을 의미한다. 만약, slackness보다 margin의 최대화가 중요하다면, C값은 커지고 반대라면 이 값은 작아진다.

우선 lagrangian을 먼저 구하면 다음과 같다.

\mathcal{L} = {1\over2}||\bold{w}||^{2} + {C\over2}\sum_{i=1}^{N}\zeta_{i}^{2} + \sum_{i=1}^{N}\alpha_{i}(1 - \zeta_{i} - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b))

KKT condition을 이용하여 주요 값들을 구하면 다음과 같은 등식을 얻을 수 있다.

\bold{w} = \sum_{i=1}^{N}\alpha_{i}y_{i}\bold{x}_{i}

\sum_{i=1}^{N}\alpha_{i}y_{i} = 0

\boldsymbol{\zeta} = {\alpha\over{C}}

마지막으로 이를 Dual Problem으로 재정의하면 다음과 같아진다.

\begin{align*} \text{maximize} \quad & -{1\over2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}(\bold{x}_{i}^{\top}\bold{x}_{j} + {1\over{C}}\delta_{ij}) + \sum_{i=1}^{N}\alpha_{i} &\\ \text{subject to} \quad & \sum_{i=1}^{N}\alpha_{i}y_{i} = 0, & \\ & \alpha_{i} \geq 0, & i = 1, ..., N \end{align*}

여기서 $\delta_{ij}$ 는 단위행렬이다. 기존 hard margin svm과 비교했을 때, ${1\over{C}}\delta_{ij}$ 외에는 바뀌지 않는 것을 알 수 있다.

L1-norm Optimization

그 다음은 L1-norm이다.

\begin{align*} \text{minimize} \quad & {1\over2}||\bold{w}||^{2} + C\sum_{i=1}^{N}\zeta_{i} &\\ \text{subject to} \quad & 1 - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b) - \zeta_{i} \leq 0, & \\ & \zeta_{i} \geq 0 & i = 1, ..., N \end{align*}

여기서는 slack variable이 반드시 0보다 크거나 같다는 것을 주의하자.

lagrangian은 다음과 같다.

\mathcal{L} = {1\over2}||\bold{w}||^{2} + C\sum_{i=1}^{N}\zeta_{i} + \sum_{i=1}^{N}\alpha_{i}(1 - \zeta_{i} - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b)) - \sum_{i=1}^{N}\beta_{i}\zeta_{i}

KKT condition을 이용하여 주요 값들을 구하면 다음과 같은 등식을 얻을 수 있다.

\bold{w} = \sum_{i=1}^{N}\alpha_{i}y_{i}\bold{x}_{i}

\sum_{i=1}^{N}\alpha_{i}y_{i} = 0

\sum_{i=1}^{N}\beta_{i} = C

마지막으로 이를 Dual Problem으로 재정의하면 다음과 같아진다.

\begin{align*} \text{maximize} \quad & -{1\over2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}\bold{x}_{i}^{\top}\bold{x}_{j} + \sum_{i=1}^{N}\alpha_{i} &\\ \text{subject to} \quad & \sum_{i=1}^{N}\alpha_{i}y_{i} = 0, & \\ & 0 \leq \alpha_{i} \leq C, & i = 1, ..., N \end{align*}

결국 기존 Hard margin과 비교했을 대는 마지막 constraint에 $\alpha_{i} \leq C$ 가 추가된 것 밖에 없다.

마지막으로 여기서 하나의 insight를 더 얻을 수 있다.
L1-norm의 optimization으로 돌아가보자.

\begin{align*} \text{minimize} \quad & {1\over2}||\bold{w}||^{2} + C\sum_{i=1}^{N}\zeta_{i} &\\ \text{subject to} \quad & 1 - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b) - \zeta_{i} \leq 0, & \\ & \zeta_{i} \geq 0 & i = 1, ..., N \end{align*}

목적 함수의 slack variable에 constraint의 값을 대입하여, 다음과 같이 변환이 가능하다.

\min {C^{\prime}\over2}||\bold{w}||^{2} + \sum_{i=1}^{N}max\{ 0, 1 - y_{i}(\bold{w}^{\top}\bold{x}_{i} + b) \}

이 형태는 logistric regression에 regularization을 수행한 것과 동일한 형태를 가지게 된다. 즉, 이전 logistic regression에서 regularization을 다루지 않았는데, 결국은 soft margin svm의 L1-norm 목적함수가 logistic regression 중에서도 hinge function이라는 것을 이용했을 때의 regularization이 되는 것이다.

Generalization

여태까지 살펴본 Regression을 통해서 우리는 General한 Classification 방식을 지정할 수 있다. 우선 아래 식을 살펴보자.

Linear Regression(Quadratic Loss)
$\min {C^{\prime}\over2}||\bold{w}||^{2} + \sum_{i=1}^{N}{1\over2}(1 - y_{i}(\bold{w}^{\top}\phi(\bold{x}_{i})) )^{2}$
Logit Regresion(Log Loss)
$\min {C^{\prime}\over2}||\bold{w}||^{2} + \sum_{i=1}^{N}\log( 1 + \exp[-y_{i}(\bold{w}^{\top}\phi(\bold{x}_{i})]) )$
Binary SVM(Hinge Loss)
$\min {C^{\prime}\over2}||\bold{w}||^{2} + \sum_{i=1}^{N}max\{ 0, 1 - y_{i}(\bold{w}^{\top}\phi(\bold{x}_{i})) \}$

여태까지 나온 식들을 살펴보면 위와 같다. 우리는 여기서 아래와 같은 일반적인 형태의 Classification을 제시할 수 있다.

General Classification
$\min {C^{\prime}\over2}||\bold{w}||^{2} + \sum_{i=1}^{N}\varepsilon\log( 1 + \exp[-y_{i}(\bold{w}^{\top}\phi(\bold{x}_{i})]) )$

여기서 $\varepsilon$ 이 1이면 바로 logistic regression이 되고, $\varepsilon$ 이 0에 수렴할 수록 SVM이 된다. 아래 그림을 보면 이를 알 수 있다.

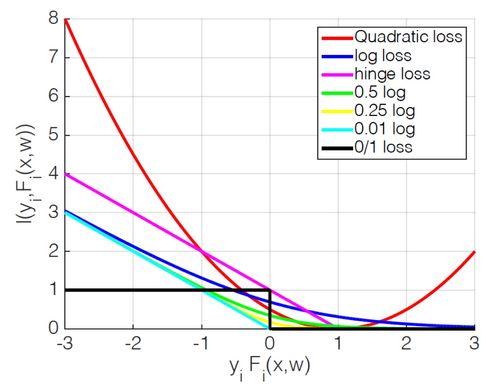
compare-regressions

Reference

Tumbnail : Photo by Markus Winkler on Unsplash