[ML] 2. Linear Regression

Intro

Regression(회귀)이라는 단어는 "원래의 상태로 돌아간다"로 돌아간다는 의미를 가진다. 결국 어떤 일련의 Event로 인해서 데이터에 Noise가 발생할 수 있어도 결국은 하나의 "보편"으로 시간이 지나면 수렴(회귀)할 것이라는 생각에 기반하는 것이다.
따라서, 우리는 이러한 "보편"을 찾기 위해서 우리가 알고 있는 독립 데이터 X를 통해서 알고자 하는 값 Y를 보편적으로 추론할 수 있다. 이 과정을 우리는 Regression이라고 부른다. 또한, X에 의해 독립적이지 않고 종속적인 Y의 관계가 Linear하게 표현될 때 이를 우리는 Linear Regression이라고 한다.
따라서, 해당 Posting에서는 Linear Regression을 바탕으로 Machine Learning이 어떻게 동작하는지를 이해하는 것이 목표이다.

Regression

정의

독립 변수 X로 부터 종속 변수 Y에 대응되는 함수 f를 생성하는 과정을 의미한다.

\bold{y} = f(\bold{x}) + \epsilon

f(\bold{x}) = \bold{w}^{\top}\bold{x}, (\bold{w} = \begin{bmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{N} \\ \end{bmatrix}, \bold{x} = \begin{bmatrix} 1 \\ x_{1} \\ x_{2} \\ \vdots \\ x_{N} \\ \end{bmatrix} )

여기서 각 변수 $x$ , $y$ , $\epsilon$ , $w$ 은 다음과 같이 여러 이름으로 불려진다.

$x$ : input, 독립 변수, predictor, regressor, covariate
$y$ : output, 종속 변수, response
$\epsilon$ : noise, 관측되지 않은 요소
$w$ : weight, 가중치, parameter

성능 평가(MSE)

우리가 만든 Regression이 얼마나 데이터를 잘 반영하는지를 알고 싶을 때, 즉 평가하고자 할 때, 우리는 Mean Squared Error(MSE)를 사용한다. 이는 이전 포스팅인 Parametric Estimation에서도 살펴보았었다.

그렇다면, MSE를 최소로 하는 f(x)는 무엇일까? 이를 통해서 또, 하나의 식견을 넓힐 수 있다. 한 번 MSE 식을 정리해보자.

\begin{align*} \Epsilon(f) &= E[||\bold{y}_*-f(\bold{x})||^2] \\ &= \int\int||\bold{y}_*-f(\bold{x})||^2p(\bold{x}, \bold{y}_*)d\bold{x}d\bold{y}_* \\ &= \int\int||\bold{y}_*-f(\bold{x})||^2p(\bold{x})p(\bold{y}_* | \bold{x})d\bold{y}_*d\bold{x} \\ &= \int p(\bold{x}) \red{\int||\bold{y}_*-f(\bold{x})||^2p(\bold{y}_* | \bold{x})d\bold{y}_*}d\bold{x} \end{align*}

여기서 중요한 것은 바로 빨간색으로 색칠한 부분이다. 우리가 바꿀 수 있는 값은 f(x)를 구성하는 w밖에 없다 즉, 위 식을 최소화하는 것은 빨간색 부분을 최소화하는 것과 같아진다.
따라서, 이 부분을 미분해서 최솟값을 구할 수 있는데 이를 확인해보자.

\begin{align*} &{\partial\over{\partial{f(\bold{x})}}}({\int||\bold{y}_*-f(\bold{x})||^2p(\bold{y}_* | \bold{x})d\bold{y}_*}) = 0 \\ &{\partial\over{\partial{f(\bold{x})}}}({\int||\bold{y}_*^2p(\bold{y}_* | \bold{x})d\bold{y}_*} - 2f(\bold{x}){\int\bold{y}_*p(\bold{y}_* | \bold{x})d\bold{y}_*} + f(\bold{x})^2{\int p(\bold{y}_* | \bold{x})d\bold{y}_*}) = 0 \\ &-2{\int\bold{y}_*p(\bold{y}_* | \bold{x})d\bold{y}_*} + 2f(\bold{x}) = 0 \\ &f(\bold{x}) = {\int\bold{y}_*p(\bold{y}_* | \bold{x})d\bold{y}_*} = E[\bold{y}_*|\bold{x}] \end{align*}

즉, 우리가 구하고자 하는 Linear Regression 함수는 data x에 따른 실제 y 값의 평균을 의미한다. Regression의 정의를 생각했을 때, 어느정도 합리적이라는 것을 알 수 있다. "보편"적이다는 의미에서 "평균"을 쓰는 경우가 많이 있기 때문이다.

위에서는 MSE를 이용해서 분석하였지만, MAE(Mean Absolute Error)를 활용하여 구할 수 있는데 이 경우에는 Regression의 형태가 또 달라진다. 즉, MSE를 최소화하는 방식은 우리가 "보편"적인 답을 구하는데 있어 "평균"을 활용한 것이고, MAE를 사용한다면, 또 다른 방식을 사용한다는 것을 알게 될 것이다.

MLE of Linear Regression

이제 Linear Regression에서 $\bold{w}$ 를 어떻게 찾아 나갈지에 대해서 살펴볼 것이다. 순서는 이전 Posting Parametric Estimation에서 살펴봤던 것과 마찬가지로 MLE, MAP 순으로 살펴볼 것이다. 그리고 이것이 왜 MLE고, MAP랑 관련이 있는지도 살펴볼 것이다.

들어가기에 앞 서, 표기법과 용어를 몇 개 정리할 필요가 있다.

$\bold{x}, \bold{y}, \bold{w}$ 등 굵은 선 처리되어 있는 변수는 vector를 의미한다.
$\bold{X}$ 등 굵고 대문자로 처리되어 있는 변수는 Matrix를 의미한다.
$\bold{w^{\top}}$ , $\bold{X}^{\top}$ 에서 T는 Transpose를 의미한다.
feature : input 데이터의 각 각 분류 기준들을 의미한다. 수식으로는 $x_1, x_2, x_3$ 이런 식으로 표현된 input들 중에 각 각의 input을 feature라고 하며, 실제 예시로는 데이터 수집 시에 각 데이터의 column(나이, 성별, 등 등)이 될 것이다.

위의 용어 정리에 의해서 다음과 같은 사실을 다시 한 번 확인하자.

먼저, 단일 Linear Regression이다.

\hat{y} = f(\bold{x}) = \bold{w}^{\top}\bold{x} = \bold{x}^{\top}\bold{w}

이번에는 여러 개의 데이터를 한 번에 추측한 결과값 $\hat{\bold{y}}$ 이다.

\hat{\bold{y}} = \bold{X}\bold{w}

각 의미를 곱씹어보면 어떻게 생겼을지 어렵풋이 짐작이 올 것이다.

basis function

여기서 또 하나 짚어볼 것은 바로 $\bold{x}$ 를 변형하는 방법이다. 바로, 우리는 데이터로 입력 받은 데이터를 바로 사용할 수도 있지만, 해당 input 값을 제곱해서 사용해도 되고, 서로 더해서 사용해도 되고, 나누어서 사용할 수도 있다. 예를 들어서 우리가 구하고 싶은 값이 대한민국 인구의 평균 나이라고 하자. 이때, 우리가 사용하는 데이터의 값이 가구 단위로 조사되어 부,모,자식1, 자식2, ... 로 분류되어 나이가 적혀있다고 하자. 이때 우리가 필요한 것은 결국 전체 인구의 나이 데이터임으로 모두 하나의 feature로 합쳐버릴 수도 있다.

이러한 과정을 위해서 우리는 basis function( $\phi(\bold{x})$ )이라는 것을 이용한다. 단순히 input data를 합성해서 하나의 input을 생성하는 것이다.

따라서, 우리는 필요에 따라 input data를 가공하여 사용하며 여러 $\phi$ 를 적용하여 나타낼 경우 linear regression은 다음과 같은 형태가 된다.

f(\bold{x}) = \bold{w}^{\top}\boldsymbol{\phi}(\bold{x})

대표적인 Basis function을 살펴보자.

Polynomial basis : 하나의 input feature에 대해서 n-제곱형태의 vector로 변환하는 형식이다. 따라서, 다음과 같이 표기 된다.
$\boldsymbol{\phi}(\bold{x}) = \begin{bmatrix} 1 \\ x \\ x^{2} \\ \vdots \\ x^{n} \\ \end{bmatrix}$ , $\bold{w}^{\top}\boldsymbol{\phi}(\bold{x}) = w_{0} + w_{1}x + w_{2}x^{2} + ... + w_{n}x^{n}$
대게 이러한 형태로 변형한 Linear Regression을 Polinomial Regression이라고 부르는데, 이를 통한 결과 값이 마치 다항식의 형태를 띄기 때문이다. 하지만, feature의 값이 polynomial이 되었더라도 $\bold{w}$ 가 선형임을 잊어서는 안된다.
이를 사용하게 되면, 우리는 1차원의 input 공간에서 선형으로는 나눌 수 없던 분류를 수행할 수 있다.
Gaussian basis : 가우시안 분포로 변환하는 것으로 특정 feature를 gaussian으로 변환하게 되면, 데이터의 경향성이 파악된다. 이는 후에 더 자세히 다룰 기회가 온다.
Spline basis: 특정 구간마다 다른 Polynomial 형태의 feature를 적용하도록 하는 방식이다. 대게 구간마다 다른 확률 분포를 적용하고자 할 때 사용한다.
Fourier basis, Hyperbolic tangent basis, wavelet basis 등 여러 가지 방식이 존재한다.

Design Matrix

마지막으로, 이렇게 만들어진 $\phi(\bold{x})$ 를 하나의 Matrix로 합친 것을 Design Matrix라고 한다. N개의 데이터를 L개의 서로 다른 basis function으로 변환한 데이터를 행렬로 표현하면, 다음과 같다.

\Phi = \begin{bmatrix} \phi_1({\bold{x_1}}) & \phi_2(\bold{x_1}) & \cdots & \phi_L(\bold{x_1}) \\ \phi_1({\bold{x_2}}) & \phi_2(\bold{x_2}) & \cdots & \phi_L(\bold{x_2}) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1({\bold{x_N}}) & \phi_2(\bold{x_N}) & \cdots & \phi_L(\bold{x_N}) \\ \end{bmatrix}

이를 통해서 표현한 모든 데이터에 대한 Linear Regression은 다음과 같다.

\hat{\bold{y}} = \Phi\bold{w}

자 이제부터 우리는 본론으로 들어와서 우리의 Linear Regression의 Weight(Parameter, $\bold{w}$ )를 어떻게 추정할 수 있을지를 알아보자.

우리는 최종적으로 우리의 Linear Regression이 정답과 매우 유사한 값을 내놓기를 원한다. 따라서, 이때 우리는 Least Square Error를 사용할 수 있다. 이는 모든 데이터에서 얻은 예측값(Linear Regression의 output)과 실제 y의 값의 Square Error의 합을 최소화하는 것이다.

\varepsilon_{LS}(\bold{w}) = {1\over2}\sum_{n=1}^{N}(y_n - \bold{w}^{\top}\boldsymbol{\phi}(\bold{x_n}))^2 = {1\over2}||\bold{y}_* - \Phi\bold{w}||^2

이제 $\argmin_{\bold{w}}\varepsilon_{LS}(\bold{w})$ 을 풀기 위해서 미분을 해보자.

\begin{align*} &{\partial\over\partial\bold{w}}{1\over2}||\bold{y}_* - \Phi\bold{w}||^2 = 0 \\ &\Phi^{\top}(\bold{y}_* - \Phi\bold{w}) = 0 \\ &\Phi^{\top}\Phi\bold{w} = \Phi^{\top}\bold{y_*} \\ &\bold{w} = (\Phi^{\top}\Phi)^{-1}\Phi^{\top}\bold{y_*} \\ &\bold{w} = \Phi^{\dagger}\bold{y_*} \end{align*}

이를 통해서, 위와 같은 식을 얻을 수 있다.

그럼 이 식이 왜 MLE랑 관련이 있는 것일까? 그것은 다음의 과정을 통해서 증명할 수 있다.

우리는 각 data마다 존재하는 error(noise, $y_* - \hat{y}$ , $\varepsilon$ )가 그 양이 많아짐에 따라 정규 분포를 따른다는 것을 알 수 있다. (Central Limit Theorem)

\begin{align*} \varepsilon &= y_* - \hat{y} = y_*-\phi(\bold{x}) \\ y_* &= \phi(\bold{x}) + \varepsilon \end{align*}

이를 좌표 평면 상에서 나타내면 다음과 같다고 할 수 있다.

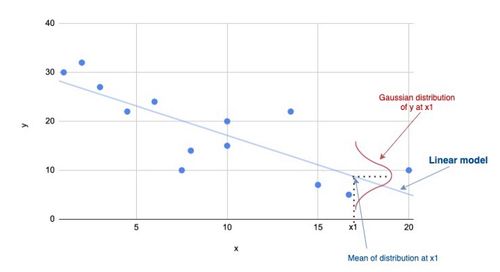
gaussian-error

또한, $\varepsilon$ 의 확률을 정의하면 다음과 같은 확률을 얻을 수 있다.

\begin{align*} p(\varepsilon) &= {1\over{\sqrt{2\pi}\sigma}}\exp{[-{\varepsilon^2\over{2\sigma^2}}]} \\ p(\varepsilon) &= {1\over{\sqrt{2\pi}\sigma}}\exp{[-{(y_*-\phi(\bold{x}))^2\over{2\sigma^2}}]} \end{align*}

여기서 우리는 $p(\varepsilon)$ 을 $p(y_*|\bold{x}; \theta)$ 라고 볼 수 있다. ( $\theta = (\bold{w}, \phi, \sigma)$ )

우리는 이를 이용해서 Likelihood를 구할 수 있다.

\begin{align*} \mathcal{L} &= \log{p(\bold{y}_*|\bold{X}; \theta)} = \sum_{i=1}^{N}{\log{p(y_{*(i)}|\bold{x}_{(i)}; \theta)}} \\ &= N\log{{1\over{\sqrt{2\pi}\sigma}}} + \sum_{i=1}^{N}{-{(y_*-\phi(\bold{x}))^2\over{2\sigma^2}}} \\ &= N\log{{1\over{\sqrt{2\pi}\sigma}}} - {1\over{\sigma^2}}\red{{1\over{2}}\sum_{i=1}^{N}{(y_*-\phi(\bold{x}))^2}} \end{align*}

우리가 변경할 수 있는 데이터는 $\phi(\bold{x})$ 밖에 없다. 따라서, 빨간색을 제외한 부분은 Likelihood의 최댓값을 구할 때, 고려하지 않아도 되는 상수로 볼 수 있다. 그렇다면, 우리는 Likelihood의 최댓값을 구하기 위해서 빨간색 표시된 부분을 최소화해야 한다는 것을 알 수 있다. 그리고, 이는 우리가 앞에서 살펴봤던, Least Squared Error와 같다.

즉, $\bold{w}_{LS}=\bold{w}_{MLE}$ 라는 것이다.

MAP of Linear Regression

이번에는 Linear Regression에서 $\bold{w}$ 를 찾아나가는 과정에서 MAP를 활용하는 과정을 알아볼 것이다.

overfitting

우리가 MLE를 통해서 Linear Regression을 찾는 것이 충분하다고 생각할 수 있다. 하지만, 우리는 어쩔 수 없이 overfitting이라는 문제에 직면하게 된다.

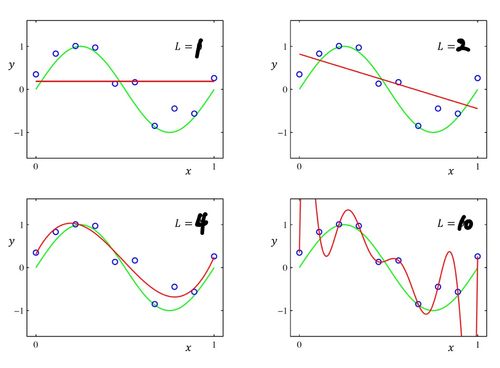
over-fitting-example

overfitting이란 데이터를 통해서 구할 수 있는 분포가 학습에 사용된 데이터에 대해서는 에러가 거의 없는 형태로 예측하지만, 그 외에 데이터에 대해서는 에러가 크게 발생하는 경우를 의미한다. 위의 예시에서 처럼 데이터가 전체 Sample space보다 턱없이 적은 경우에 발생하기 쉽다.

이러한 문제는 사실 basis function을 잘 선택하면 해결할 수 있다. 하지만, 우리가 어떻게 매번 적절한 basis function을 찾기 위해서 iteration을 반복하는 것이 올바를까? 그리고 이는 실제 적합한 값을 찾기 위한 수학적 식도 존재하지 않는다.

Regularization

따라서, 우리는 regularization을 수행한다. 위의 overfitting된 그래프를 보면 하나의 insight(번뜩이는 idea?)를 얻을 수 있다. 바로, 급격한 기울기의 변화는 overfitting과 유사한 의미로 볼 수 있다는 것이다. 즉, 그래프의 형태가 smooth 해야한다는 것이다.

따라서, 우리는 하나의 error에 대해서 다음과 같이 재정의해서 smoothing(regularization)을 수행할 수 있다.

\varepsilon = {1\over2}||\bold{y}_* - \Phi\bold{w}||^2 + {\lambda\over{2}}||\bold{w}||^2

$\bold{w}$ 의 L2 norm을 error에 추가하여 $\bold{w}$ 의 크기가 작아지는 방향으로 예측을 할 수 있도록 하는 것이다. (물론 L1 norm을 사용할 수도 있다. 이 또한, 후에 다룰 것이니 여기서는 넘어가겠다. 추가로 이렇게 L2 norm을 이용하면 Ridge Regression, L1 norm을 이용하면 Lasso Regression이라고 한다.)

자 이제 위의 식을 미분해서 최소값이 되게 하는 $\bold{w}$ 를 찾아보자. 과정은 연산이 그렇게 어렵지 않으므로 넘어가고 결과는 아래와 같다.

\bold{w}_{ridge} = (\lambda I + \Phi^{\top}\Phi)^{-1}\Phi^{\top}\bold{y}_*

그럼 이 역시 MAP를 통해서 해석해보도록 하자.

위에서 살펴본 바와 같이 우리는 w값이 작을 확률이 높을 수록 좋은 성능을 가질 것이라는 Prior를 얻을 수 있다.

즉, $p(\bold{w})$ 가 zero-mean gaussian(표준정규분포)형태를 이루기를 바랄 것이다.

p(\bold{w}) = \mathcal{N}(\bold{w}|0, \Sigma)

그리고, 이전에 MLE를 구할 때, Likelihood를 다음과 같이 정의했다.

\begin{align*} p(\bold{y}_*|\bold{X}; \theta) &= \mathcal{N}(\bold{y}_*-\Phi\bold{w}, \sigma I) \\ p(\bold{y}_*|\Phi, \bold{w}) &= \mathcal{N}(\bold{y}_*-\Phi\bold{w}, \sigma I) \end{align*}

따라서, 우리는 이를 이용해서 posterior를 추론할 수 있다.

p(\bold{w}|\bold{y}_*, \Phi) = {{p(\bold{y}_*| \Phi, \bold{w})p(\bold{w})}\over{p(\bold{y}_*|\Phi)}}

여기서 MAP를 구할 때에는 Lemma 정리(두 정규분포의 conditional Probability를 구하는 공식)를 이용하면 편하다. 따로 연산은 수행하지 않지만 결과 값은 아래와 같다.

\bold{w}_{MAP} = (\sigma^2\Sigma^{-1}+\Phi^{\top}\Phi)^{-1}\Phi^{\top}\bold{y}

여기서 만약 우리가 $\Sigma = {\sigma^2\over{\lambda}}I$ 라고 가정하면, 위의 MAP 식은 Ridge Regression과 동일해지는 것을 알 수 있다.

즉, Ridge Regression은 MAP의 한 종류라고 볼 수 있는 것이다.

\bold{w}_{ridge} \in {(\bold{w}_{MAP}, \Sigma)}

Gradient Descent

여태까지 우리는 Loss를 정의하고, 이 Loss가 최솟값을 갖는 $\bold{w}$ 를 찾는 것을 목표로 하였다. 하지만, 우리가 다루는 모든 Loss가 미분이 항상 쉬운 것은 아니다. 뿐만 아니라, Loss의 미분 값이 5차원 이상의 식으로 이루어진다면, 우리는 이를 풀 수 없을 수도 있다. 5차원 이상의 polynomial에서는 선형대수적인 해결법(근의 방정식)이 없다는 것이 증명되어있다.(Abel-Ruffini theorem)

따라서, 우리는 Loss가 0이 되는 지점을 찾기 위해서, w의 값을 점진적으로 업데이트하는 방식을 활용한다. 이때, 우리는 w의 값이 계속해서 Loss를 감소시키기를 원한다. 따라서, 우리는 현재 $\bold{w}$ 에서 Gradient를 현재 $\bold{w}$ 에 빼준다. 이를 우리는 Gradient Descent라고 한다.

\bold{w}_{t+1} = \bold{w}_{t} - \gamma((\nabla L)(\bold{w}_{t}))^{\top}

여기서 $\gamma$ 는 step size(learning rate)라고 하며, 기울기값을 얼마나 반영할지를 의미한다.

이제부터는 Gradient Descent를 더 효과적으로 진행하기 위한 3가지의 기술들을 추가적으로 제시한다.

1. optimize stepsize

stepsize( $\gamma$ )가 특정 상수로 제시된 게 아니라 변수로 표현된 이유는 linear regression마다 적절한 $\gamma$ 가 다르기 때문이다. 하나의 예시를 들어보자.

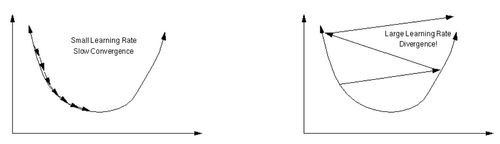
loss-divergence

위는 Loss function이 convex할 때, 최솟값을 찾아나가는 과정이다. 만약, $\gamma$ 가 크다면, Loss가 특정값으로 수렴하는 것이 아니라 발산하는 것을 알 수 있다. 이를 막기 위해 $\gamma$ 를 굉장히 작은 수로 하는 경우에는 Loss의 최솟값을 찾기도 전에 특정 지점에서 멈춰버릴 수도 있다. 또한, Loss의 graph형태는 data마다 달라지기 때문에 절대적인 $\gamma$ 역시 존재하지 않는다.

따라서, 우리는 매 update마다 적절한 $\gamma$ 를 찾을려고 노력한다. 여기서는 자세히 다루지 않지만 후에 더 다룰 기회가 있을 것이다. 간단히 프로그래밍적으로(systemical) 생각하면, 업데이트 이후 loss가 만약 그전 Loss보다 커진다면, 이를 취소하고 더 작은 $\gamma$ 를 사용하도록 하고, 업데이트 된 후의 Loss와 그전 Loss가 같다면, 진짜 수렴하는지를 확인하기 위해서 $\gamma$ 를 키워볼 수도 있다.

2. momentum

우리가 Gradient Descent를 진행하다보면, 다음과 같은 현상을 자주 마주하게 된다.

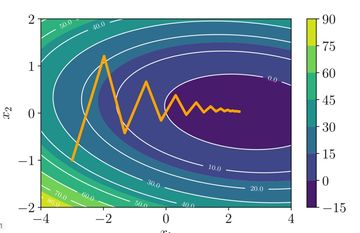
momentum-example-1

우리가 찾고자 하는 Loss를 찾아가는 과정에서 매 업데이트마다 반대방향으로 기울기가 바뀌는 경우이다.(진동한다) 이는 최종으로 찾고자 하는 값을 찾는 과정이 더 오래 걸리게 한다. 따라서, 우리는 이러한 진동을 막기 위해서 Momentum을 사용한다. 즉, 이전 차시에서의 gradient를 저장해두고, 이를 더해서 진동하는 것을 막는 것이다.

\bold{w}_{i+1} = \bold{w}_{i} - \gamma_{i}((\nabla L)(\bold{w}_{i}))^{\top} + \alpha \Delta \bold{w}_i ,( \alpha \in [0, 1] )

\Delta \bold{w}_i = \bold{w}_{i} - \bold{w}_{i-1} = \alpha \Delta \bold{w}_{i-1} - \gamma_{i-1}((\nabla L)(\bold{w}_{i-1}))^{\top}

즉, 그림으로 표현하면, 다음과 같다.

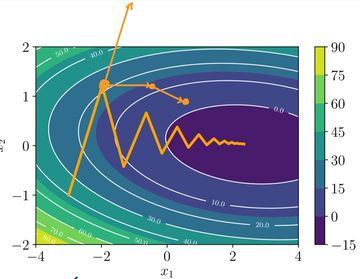
momentum-example-2

이전 변화량과 현재 변화량을 합하여 이동하기 때문에 위에 새로 추가된 것처럼 진동하지 않고, 진행하는 것을 볼 수 있다.

3. Stochastic Gradient Descent

우리의 Gradient Descent의 가장 큰 문제는 바로 Global Minimum을 찾을 거라는 확신을 줄 수 없다는 것이다. 아래 그림을 보자.

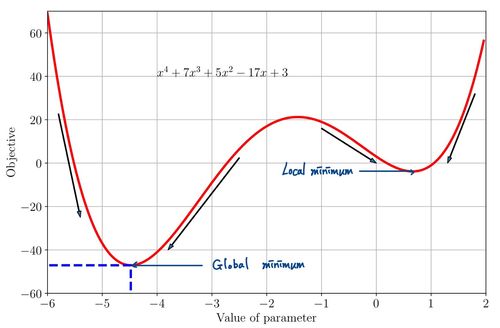
gradient-descent-example

여기서 우리는 초기 w 값을 어떻게 정하냐에 따라서, local minimum을 얻게 되거나 global minimum을 얻게 된다. 즉, 초기값이 결과에 굉장히 큰 영향을 준다는 것이다.

이를 해결할 수 있으며, 학습 효율도 높일 수 있는 것이 Stochastic Gradient Descent이다. 원리는 Loss를 구하기 위해서 전체 데이터(모집단)를 사용했었는데 그러지말고 일부 데이터를 랜덤하게 추출(sampling)해서(표본 집단) 이들을 통해서 Loss function을 구하기를 반복하자는 것이다.

이 방식을 통해서 구한 Gradient의 평균이 결국은 전체 batch의 평균과 같다는 것은 Central Limit Theorem(중심 극한 정리)에 의해 증명이 된다. 따라서, 우리는 이를 통한 gradient descent도 특정 minimum을 향해 나아가고 있음을 알 수 있다.

그렇지만, 표본 집단을 이용한 평균을 구했을 때에 우리는 noise에 의해서 local minimum으로만 수렴하는 현상을 막을 수 있다. 즉, gradient descent를 반복하다보면, 다른 local minimum으로 튀어나가기도 하며 global minimum을 발견할 확률을 높일 수 있는 것이다.

Reference

Tumbnail : Photo by Markus Winkler on Unsplash
Probabilistic interpretation of linear regression clearly explained, Lily Chen