Intro
Machine Learning은 특정 목표를 달성하기 위해서 데이터로 부터 pattern 또는 가정 등을 유도해내는 방법이다.
이를 위한 가장 일반적인 방법은 여러 개의 확률분포와 이것의 parameter의 조합(probabilistic model)들 중에서 측정된 데이터들을 가장 잘 나타내는 하나를 찾아내는 것이다.
그 중에서, 확률 분포를 결정한 상태에서 parameter를 찾아나가는 형태의 접근법을 우리는 Parametric Estimation이라고 한다. 그 외에도 Nonparametric, Semi-parametric 방식도 존재하지만 이는 여기서는 다루지 않는다.
Small Example
간단한 예시를 통해서 Parametric Estimation의 흐름을 익혀보자.
한 학급에서 학생들의 형제자매 수에 대한 예측을 하고 싶다고 하자.
그렇다면, 우리는 먼저 조사(관측)를 수행해야 한다. 이를 통해서 다음과 같은 데이터를 얻게 되었다고 하자.
| x | 1 | 2 | 3 | 4 | 5 | 6 | x≥7 |
|---|
| p(X=x) | 17 | 59 | 15 | 6 | 2 | 0 | 1 |
여기서 우리는 여러 사전 지식을 활용하여 해당 데이터를 보았을 때, 해당 분포가 Poisson 분포의 형태라는 것을 알 수 있다.
따라서, 우리는 해당 분포를 Poisson이라고 가정한 다음에는 단순히 해당 분포에 대입하며, 가장 적절한 parameter만 찾으면 된다.
이 과정과 단순히 각 x에서의 확률값을 구하는 방식이랑 무엇이 다른지를 알아야지 해당 과정의 의의를 알 수 있다.
먼저, 우리가 하고자 하는 일이 형제자매의 평균 수를 구한다고 하자. 이때의 평균 값과 Poisson 분포에서의 확률값은 다를 수 밖에 없다.
이렇게 확률 분포를 구하는 것의 의미는 이것말고도 보지 않은 데이터(unseen data)를 처리함에 있다. 우리가 만약 모든 가능한 경우의 수를 모두 알고 있고, 이를 저장할 공간이 충분하다면,
이러한 확률 분포를 구할 필요가 없다. 하지만, 우리가 원하는 추측은 unseen data에 대해서도 그럴사해야 한다. 이를 위해서는 결국 확률 분포가 필요하다.
위의 예시에서 만약, 형제자매가 3명인 경우의 데이터가 없다고 하자. 이 경우에도 확률분포를 통한 추측을 한다면, 우리는 유의미한 값을 구할 수 있는 것이다.
Parametric Estimation
정의
sample space Ω에서 통계 실험의 관측 결과를 통해서 얻은 sample X1, X2, ... , Xn이 있다고 하자. 각 sample에 대한 확률 분포를 우리는 pθ라고 한다.
여기서 θ는 특정 확률 분포에서의 parameter를 의미한다. 만약, bernoulli 라면, 단일 시행에 대한 확률이 될 것이고, binomial이라면, 단일 시행의 확률과 횟수가 해당 값이 될 것이다.
성능 평가
여기서 우리가 찾기를 원하는 것은 전체 sample space Ω를 모두 잘 표현할 수 있는 θ∗(실제 true θ)를 찾는 것이다.(이미 확률 분포의 형태(함수, ex. Bernoulli, Binomial)는 이미 정의되어 있다.)
그렇다면, 실제 θ∗와 추측을 통해 만든 θ^ 사이의 비교를 위한 지표도 필요할 것이다. 즉, 우리가 만든 확률 분포의 예측 성능평가가 필요하다는 것이다. 이를 측정하기 위해서 우리는 Risk라는 것을 사용한다.
간단하게도 실제 θ∗와 θ^의 Mean Square Error를 계산한다.
Risk=E[(θ^−θ∗)2]=E[θ^2−2θ^θ∗+θ∗2]=E[θ^2]−2θ∗E[θ^]+θ∗2=E[θ^2]−2θ∗E[θ^]+θ∗2+(E2[θ^]−E2[θ^])=(E[θ^]−θ∗)2+E[θ^2]−E2[θ^]=Bias2+Var[θ^]
해당 식을 분석해보면, 이와 같은 의미로 해석하는 것이 가능하다. 우리가 특정 확률 분포의 파라미터를 단 하나로 단정하고 Risk를 계산하는 경우는 Variance 값은 0이다. 즉, 해당 확률 분포가 가지는 Risk는 단순히 해당 parameter와 실제 parameter가 얼마나 찾이가 나는가를 의미한다.
하지만, parameter를 특정하지 않고, 범위로 지정한다면, (예를 들어, 주사위를 던져 3이 나올 확률은 1/6 ~ 1/3이다.) 해당 확률의 평균과 Variance가 영향을 미칠 것이다.
다소 처음에는 헷갈릴 수 있지만, 해당 식에서 평균이 의미는 잘 확인하자. 특정 확률 분포를 가지도록 하는 θ가 θ∗ 에 얼마나 근접한지를 확인하기 위한 식이라는 것을 다시 한 번 기억하자.
Estimation
이제부터는 앞에서 살펴보았던, parameteric estimation에서 어떻게 θ^를 구할 수 있는지를 다룰 것이다. 확률/통계 이론에서는 크게 3가지로 나눌 수 있다고 볼 수 있다. 각 각을 살펴보도록 하자.
1. MLE
Maximum Likelihood Estimation의 약자이다. 여기서, Likelihood는 가능성이라는 뜻을 가지며, 확률/통계 이론에서 이는 확률을 해당 사건이 발생할 가능성으로 해석하는 것이다. 이를 이용해서 우리가 풀고자 하는 문제, 우리가 추측한 θ가 우리가 가진 Dataset를 만족시킬 가능성을 확인하기 위해 사용한다. 아래 수식을 보자.
L(θ;D)=p(D∣θ)=p(x1,x2,...,xn∣θ)=i=1∏np(xi∣θ)
(위 식을 이해하려면, 먼저 Dataset의 각 data들은 서로 independent하다는 사실을 기억하자.)
결국 θ가 주어졌을 때, Dataset일 확률을 구하는 것이다. 이를 다시 생각하면, θ가 얼마나 데이터셋의 확률을 잘 표현할 수 있는가와 같다.
이것을 직관적으로 이해하려면 하나의 예시를 보면 좋다.
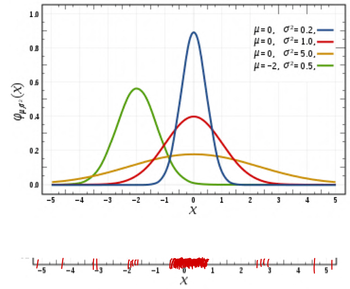
첫 번째 그래프는 같은 가우시안 분포 함수를 쓰면서, parameter만 다르게 한 경우이고, 아래는 실제 데이터의 분포라고 하자.(빨간색 선 하나 하나가 데이터를 의미)
이때, Likelihood를 각 각 구하면 각 x에서의 확률분포의 확률값을 모두 곱하면 된다. 그 경우 어떤 것이 제일 클지는 분명하다. 바로 파란색 분포일 것이다.
그렇다면, 우리가 원하는 것은 무엇인가? 바로 가장 높은 가능성을 가지게 하는 θ를 찾는 것이다. 따라서, 이를 식으로 표시하면 아래와 같다.
θ^MLE=θargmaxL(θ;D)
여기서 하나 문제가 있을 수 있다. 바로, 컴퓨터로 연산하게 되면 underflow가 발생하는 것이다. 특정 언어가 계산할 수 있는 소수점 범위를 벗어난다면, 제대로 된 결과를 얻을 수 없다. 이와 같은 문제를 vanishing likelihood라고 한다.
따라서, 우리는 log를 취했을 때와 log를 취하지 않았을 때의 경향성이 같음을 바탕으로 likelihood에 log를 취한 값을 이용하여 MLE를 구하는 것이 일반적이다. 이 방식을 maxmum log likelihood estimation 이라고 부른다.
l(θ;D)=i=1∑nlog(p(xi∣θ))
이 방식을 이용하게 되면, 곱셈이 모두 덧셈으로 바뀌기 때문에 계산에서도 용이하다.
여기까지 살펴보면, 하나의 의문이 들 수도 있다. 바로, p(θ∣D)도 측정 기준으로 사용할 수 있지 않냐는 것이다. 이 역시도 Dataset이 주어질 때, θ일 확률이라고 볼 수 있다.
어찌보면, 사람의 생각으로는 이게 더 당연하게 느껴질 수도 있다. 이는 바로 다음 MAP에서 다룰 것이다. 우선 MLE를 먼저한 이유는 이것이 더 구하기 쉽기 때문임을 기억해두자.
1 🤔 증명
2
3 (*해당 내용은 정보 이론에 기반한 MLE에 대한 추가적인 이해를 위한 내용입니다. 해당 내용은 자세히 알 필요까지는 없습니다.)
4
5 두 확률 분포 간 information Entropy의 차이를 나타내는 KL divergence의 최솟값을 구하는 것이 우리의 목표라고 정의할 수 있다.
6 따라서, 우리가 결국 얻고자 하는 것은 확률 분포 함수가 주어졌을 때,
7 n이 무한대로 갈 때, 경험적 확률(empirical probability)에 가장 근사하는 parameter를 찾는 것이다.
8 따라서, 우리는 KL divergence의 최솟값을 구하면 된다.
θargminKL(p~∣∣pθ)=θargmin∫p~(x)logpθ(x)p~(x)dx=θargmin[−∫p~(x)logp~(x)dx−∫p~(x)logpθ(x)dx]=θargmax∫p~(x)logpθ(x)dx=θargmaxi=1∑nlogpθ(xi)=θMLE
2. MAP
Maximum A Posteriori의 약자이다. Posteriori는 사후 확률이라고도 부르며, dataset이 주어졌을 때, θ일 확률을 구하는 것이다.
이를 바로 구하는 것은 다소 어렵다. 왜냐하면, Dataset이 조건으로 들어가는 형태이기 때문이다. (p(θ∣D))
따라서, 우리는 Bayes' Theorem에 따라서 이전에 배운 Likelihood와 parameter의 확률, 그리고 Dataset의 확률을 활용히여 풀어낼 것이다.
p(θ∣D)=p(D)p(D∣θ)p(θ)
여기서 주의해서 볼 것은 바로 p(θ∣D)와 p(θ)의 관계이다. dataset이 주어질 때의 parameter의 확률을 구하기 위해서 원래 parameter의 확률이 필요하다는 것이다.
어찌보면 굉장히 모순되어 보일 수 있지만, 우리가 이것을 사전 확률(priori)로 본다면 다르게 볼 여지가 있다.
예를 들면, 우리가 수상한 주사위로 하는 게임에 참가한다고 하자. 이때, 우리는 수상한 주사위의 실제 확률은 알 수 없지만, 주사위 자체의 확률은 모두 1/6이라는 것을 알고 있다. 따라서, p(θ=61)=α,p(θ=61)=β 라고 할 수 있다. 만약 정말 수상해보인다면, 우리는 α가 점점 작아진다는 식으로 표현할 수 있고, 하나도 수상해보이지 않는 일반 주사위라면, α=1,β=0으로 할 수도 있다. 이 경우에는 likelihood 값에 상관없이 다른 모든 값이 0이기 때문에 결국은 p(θ∣D)=p(θ) 가 되는 것을 알 수 있다.
최종적으로, MAP도 결국은 Dataset을 얼마나 parameter가 잘 표현하는가에 대한 지표로 사용할 수 있다.
따라서, 이를 최대로 만드는 parameter는 θ∗와 굉장히 근접할 것이다.
θ^MAP=θargmaxp(θ∣D)=θargmaxp(D)p(D∣θ)p(θ)=θargmaxp(D∣θ)p(θ)=θargmax[logp(D∣θ)+logp(θ)]
MLE와 마찬가지로 이 또한 연산 및 vanishing을 막기 위해서 log를 취한다. 사실상 likelihood와 사전 확률의 합을 최대로 하는 θ를 찾는 것이다.
3. Bayesian Inference
이제 마지막 방법으로 제시되는 Bayesian Inference이다. 이는 대게 Bayesian Estimation이라고 많이 불리는 것 같다. 이전까지 MLE, MAP는 결국 주어진 식을 최대로 하는 확정적 θ 하나를 구하는 것을 목표로 했다.
Bayesian Inference는 Dataset이 주어졌을 때, θ의 평균값을 활용한다. 더 자세히 말하면, Posteriori(사후 확률)의 평균을 구하는 것이다.
이를 구하는 과정을 살펴보면 이해하는데 도움이 될 것이다. 한 번 살펴보자.
θ^BE=E[θ∣D]=∫01θp(θ∣D)dθ=∫01θp(D)p(D∣θ)p(θ)dθ=p(D)∫01θp(θ)p(D∣θ)dθ=p(D)∫01θp(θ)∏i=1np(xi∣θ)dθ=∫01p(D∣θ)p(θ)dθ∫01θp(θ)∏i=1np(xi∣θ)dθ=∫01p(θ)∏i=1np(xi∣θ)dθ∫01θp(θ)∏i=1np(xi∣θ)dθ
이를 구하는 과정은 이전과는 다르게 상대값이 아닌 평균을 구해야하기 때문에 posteriori(사후 확률,p(θ∣D))를 구해야 한다.
하지만, 여기서 잡기술이 하나 존재한다. 바로 Conjugate Prior이다.
바로 두 확률 분포 함수(likelihood, prior)에 의한 posterior의 형태가 정해진 경우가 있기 때문이다.
| Prior p(θ∣α) | Likelihood p(D∣θ) | Posterior p(θ∣D,α) | Expectation of Posterior |
|---|
| Beta (α,β) | Benoulli (∑i=1nxi) | Beta (α+∑i=1nxi,β+n−∑i=1nxi) | α+β+nα+∑i=1nxi |
| Beta (α,β) | Binomial (∑i=1nNi,∑i=1nxi) | Beta (α+∑i=1nxi,β+∑i=1nNi−∑i=1nxi) | α+β+∑i=1nNiα+∑i=1nxi |
| Gaussian (μ0,σ02) | Gaussian (μ,σ2) | Gaussian (σ021+σ2n1(σ02μ0+σ2∑i=1nxi),(σ021+σ2n)−1) | σ021+σ2n1(σ02μ0+σ2∑i=1nxi) |
이를 이용하면, 우리는 간단하게 Posteriori의 평균을 구할 수 있다.
Reference

Comments