[ML] 5. Multiclass Classification in SVM

Intro

이전 Posting에서는 SVM에 대해서 알아보았다. 일반적인 Logistic Regression에서는 softmax function을 통해서 여러 class를 구분할 수 있었지만, SVM의 경우 구분 선이 결국은 hyperplane으로만 표현 가능하다. 이를 해결하기 위한 SVM에서의 여러 해결책을 알아보자.

Multiclass in SVM

가장 쉽게 생각할 수 있는 것은 SVM을 결합해서 Multiclass를 구분할 수 있다는 idea이다. 아래에서 곧바로 제시할 아이디어들이 이에 대한 내용이다.

1. OvR SVM

One vs Rest 의 약자로 다양한 별명이 존재한다. (One vs All, OVA, One Against All, OAA)
이름에서부터 느껴지다시피 하나의 class와 그 외에 모든 class를 하나로 묶어서 SVM을 총 class 갯수만큼 만들어서 각 decision boundary로 부터 거리가 양의 방향으로 가장 큰 class를 선택하는 방식이다.

\argmax_{k \in [K]}(\bold{w}_{(k)}^{\top}\phi(\bold{x})+ b_{(k)})

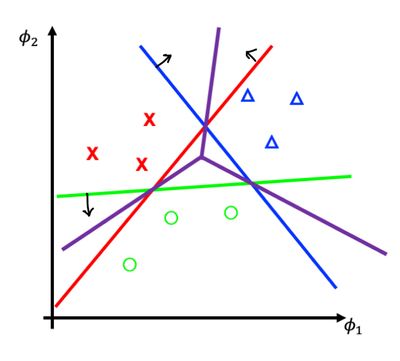
svm-ovr

이 방식은 하나의 큰 문제를 갖고 있는데, 그것은 과도한 데이터 불균형을 유발한다는 것이다. 이러한 문제는 class의 수가 많아질 수록 더 심해진다.

2. OvO SVM

One vs (Another) One의 약자로, 해당 방식은 1대1로 비교하면서 각 SVM에서 선택한 class 중에서 가장 많은 선택을 받은 class를 최종한다. OvR과는 다르게 각 각의 class를 1대1로 비교하기 때문에 데이터의 불균형에 대한 위협은 덜하다. 하지만, 해당 과정을 수행하기 위해서는 총 K(K-1)/2개의 SVM이 필요하다.

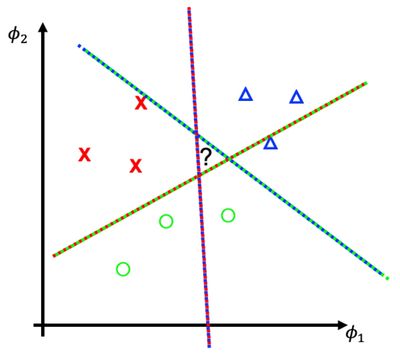
svm-ovo

또한, 그림에서 "?"로 표시된 부분을 어떤 class로 선택할지에 대한 기준이 없다. 왜냐하면, 각 영역에서 한 표씩만 받기 때문이다.

3. DAG SVM

앞 서 보았던 OvO와 OvR의 문제를 해결하기 위해서 장단점을 취하기 위해서 둘을 결합한 방식이다. 계층 형태로 SVM을 구성하기 때문에 OvO보다는 적은 SVM을 사용하면서, OvO에서의 과도한 데이터 불균형을 해결한다.

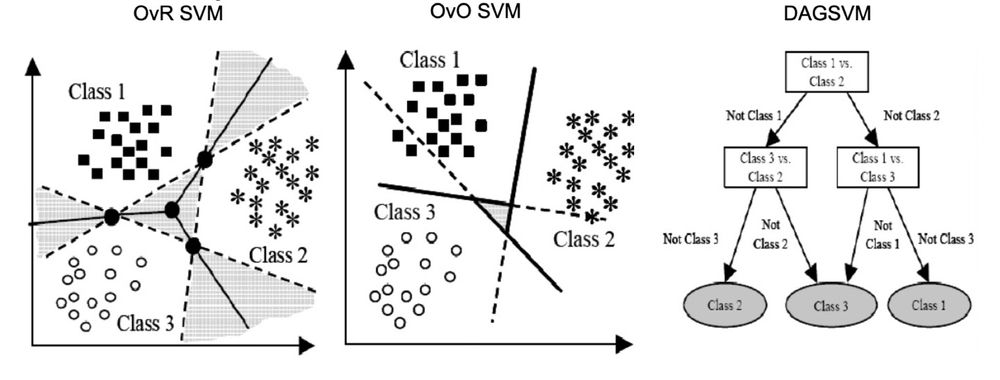
svm-multiclass-comparing

4. WW SVM

multiclass 구분을 SVM 최적화 과정에 적용하기 위해서 목적 함수의 형태를 변형하여 구현한 방법으로 자세히 다루지 않지만, 궁금하다면 해당 🔗 link를 통해서 확인할 수 있다.

Kernel Method

이전까지는 실제로 SVM의 형태를 변형시키거나 SVM을 여러 개 활용하여 multiclass classification을 수행하기 위한 방법을 보았다.

또 다른 방법이 존재한다. 바로 input 공간을 확장하는 것이다. 즉, 더 많은 유의미한 feature를 수집하거나 기존 feature를 가공하여 새로운 feature로 활용하는 것이다. 시스템적으로 해결할 수 있는 방법은 기존 feature를 가공하여 새로운 feature를 활용하는 것이다. 아래의 예시를 보자.

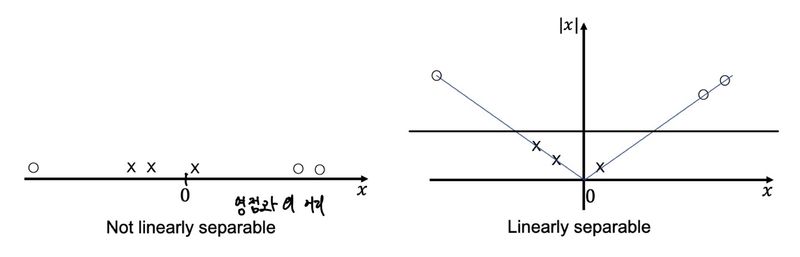
feature-transposing

왼쪽 공간에서는 SVM은 decision vector를 적절하게 선택하는 것이 어렵다. 하지만, 기존 x 데이터에 절대값을 취하여 나타내어 데이터에 추가하면, 쉽게 decision boundary를 결정하는 것을 볼 수 있다. 그렇다면, 이러한 여러 변환 함수를 적용해보며 여러 feature를 더 추출하는 것이 좋은 해결책을 가져다 줄 것이다.

그렇다면, 우리의 Soft margin SVM의 Dual Problem을 다시 한 번 살펴보자.

\begin{align*} \text{maximize} \quad & -{1\over2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}\bold{x}_{i}^{\top}\bold{x}_{j} + \sum_{i=1}^{N}\alpha_{i} &\\ \text{subject to} \quad & \sum_{i=1}^{N}\alpha_{i}y_{i} = 0, & \\ & 0 \leq \alpha_{i} \leq C, & i = 1, ..., N \end{align*}

이것을 feature 변환(basis function을 취한다.)을 통해서 다음과 같이 변형한다는 것이다.

\begin{align*} \text{maximize} \quad & -{1\over2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_{i}\alpha_{j}y_{i}y_{j}\red{\boldsymbol{\phi}^{\top}(\bold{x}_{i})\boldsymbol{\phi}(\bold{x}_{j})} + \sum_{i=1}^{N}\alpha_{i} &\\ \text{subject to} \quad & \sum_{i=1}^{N}\alpha_{i}y_{i} = 0, & \\ & 0 \leq \alpha_{i} \leq C, & i = 1, ..., N \end{align*}

하지만, 우리가 새로운 feature를 생성할 수록, 그리고 기존 feature를 복잡하게 사용할 수록 $\boldsymbol{\phi}(\bold{x}_{i})$ 를 연산하는 비용이 커질 수 밖에 없다.

따라서, 우리는 일종의 trick을 하나 사용하도록 한다. 바로, 매 bayese update 마다 변하지 않고 재사용되는 값인 $\boldsymbol{\phi}^{\top}(\bold{x}_{i})\boldsymbol{\phi}(\bold{x}_{j})$ 를 다른 값으로 대체하면 어떨까? 그렇게 하면 우리는 $\boldsymbol{\phi}(\bold{x}_{i})$ 를 계산하고 구성하는 수고를 덜 수 있다.

이것이 kernel method(trick)의 핵심 아이디어이다.

가장 대표적인 예시로 아래와 같은 복잡한 $\phi$ 가 주어졌을 때,

\boldsymbol{\phi}(x) = \exp[{{-x^{2}}\over{2\sigma^{2}}}](1, \sqrt{1\over{1!\sigma^{2}}}x, \sqrt{1\over{2!\sigma^{4}}}x^{2}, \sqrt{1\over{3!\sigma^{6}}}x^{3}, \cdots)

아래의 (RBF) kernel로 대체가 가능해진다.

\kappa(x,x^{\prime}) = \exp(-{{(x - x^{\prime})}\over{2\sigma^{2}}}) = \boldsymbol{\phi}^{\top}(x)\boldsymbol{\phi}(x^{\prime})

대게 우리가 표현하고자 하는 형태의 $\boldsymbol{\phi}$ 는 이미 특정 kernel 함수로 매핑되고 있으니 직접 $\boldsymbol{\phi}$ 를 계산하기 전에 찾아보는 것이 도움이 될 것이다.🔗 link

Reference

Tumbnail : Photo by Markus Winkler on Unsplash
A Comparison of Methods for Multi-class Support Vector Machines, Chih-Wei Hsu and Chih-Jen Lin, https://www.csie.ntu.edu.tw/~cjlin/papers/multisvm.pdf
SEVEN MOST POPULAR SVM KERNELS, https://dataaspirant.com/svm-kernels/#t-1608054630726

[ML] 5. Multiclass Classification in SVM

Intro

Multiclass in SVM

Kernel Method

Reference

Comments

Related Posts